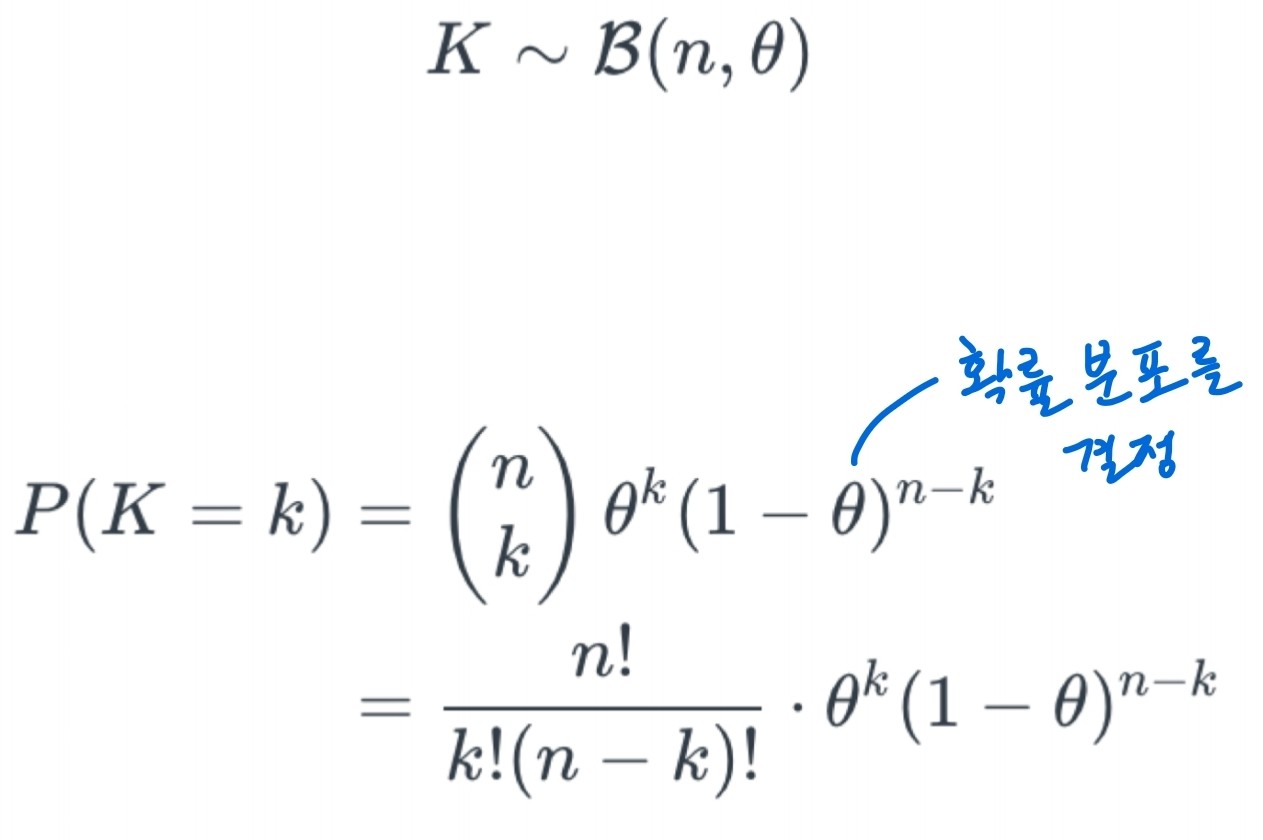모두를 위한 딥러닝 2 - Lab7-1: Tips
모두를 위한 딥러닝 Lab7-1: Tips 강의를 본 후 공부를 목적으로 작성한 게시물입니다.
Maximum Likelihood Estimate(MLE)
Probalility vs Likelihood
Probalility(확률)는 우리가 잘 알고 있듯이 어떤 관측값이 발생할 정도를 뜻하는데, 이는 다르게 말하면 한 확률분포에서 해당 관측값 또는 관측 구간이 얼마의 확률을 가지는가를 뜻한다. 이에 반해 Likelihood(우도, 가능도)는 이 관측값이 주어진 확률 분포에서 확률이 얼마나 되는지를 말한다.
중요한 차이점은 확률은 이미 배경이 되는 확률 분포가 고정되어 있고, 우도는 고정되어 있지 않다는 것이다.
MLE
이런 의미를 가진 우도를 최대화 한다는 것은 관측된 결과에 맞는 확률 분포를 찾아낸다는 것으로 생각할 수 있다.
베르누이 분포를 예로 들면 확률분포를 결정하는 아래와 같은 상황에서 $\theta$를 변화시키면서 주어진 값에 맞춰 확률 분포를 최적화 하는 것이다.
최적화 하는 과정은 마찬가지로 gradient descent(ascent)를 통해 진행한다.
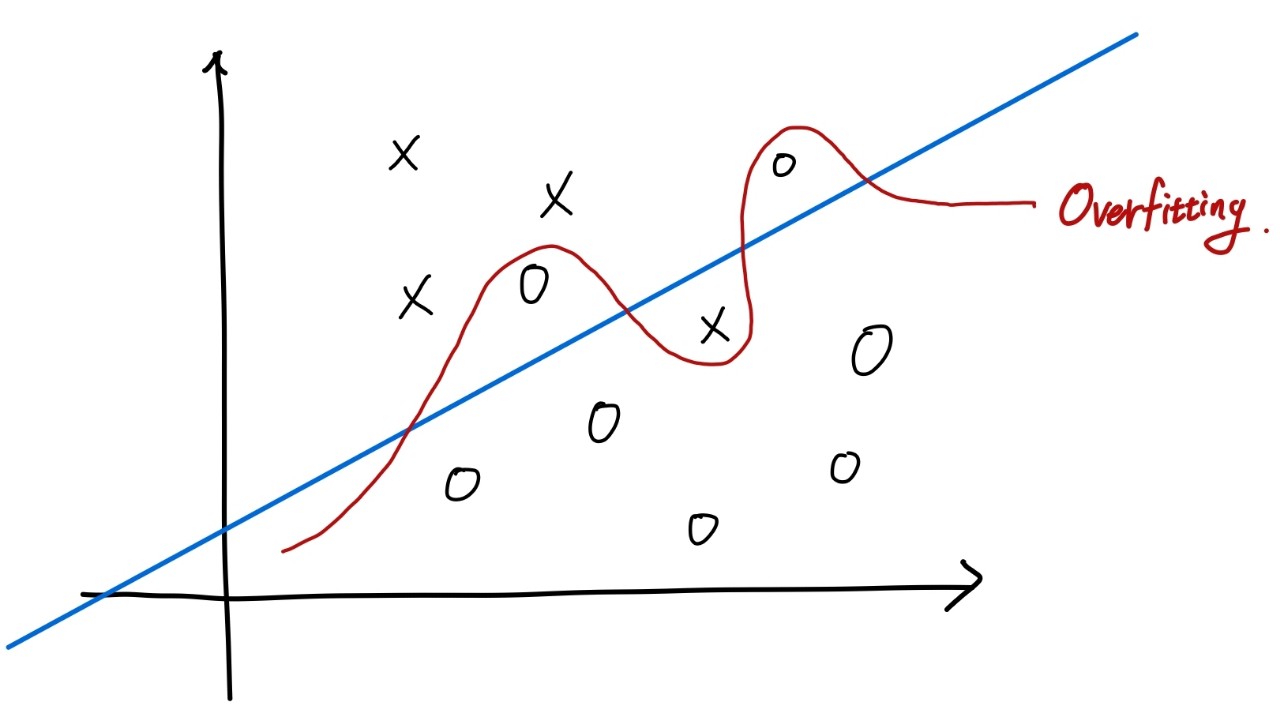
Overfitting
아래와 같이 Train set에 대해 과하게 맞춰 학습한 것을 말한다. 이 경우 학습할 때 사용한 데이터 셋이 아닌 데이터가 주어졌을 때의 예측 성능이 급격하게 떨어지게 된다.
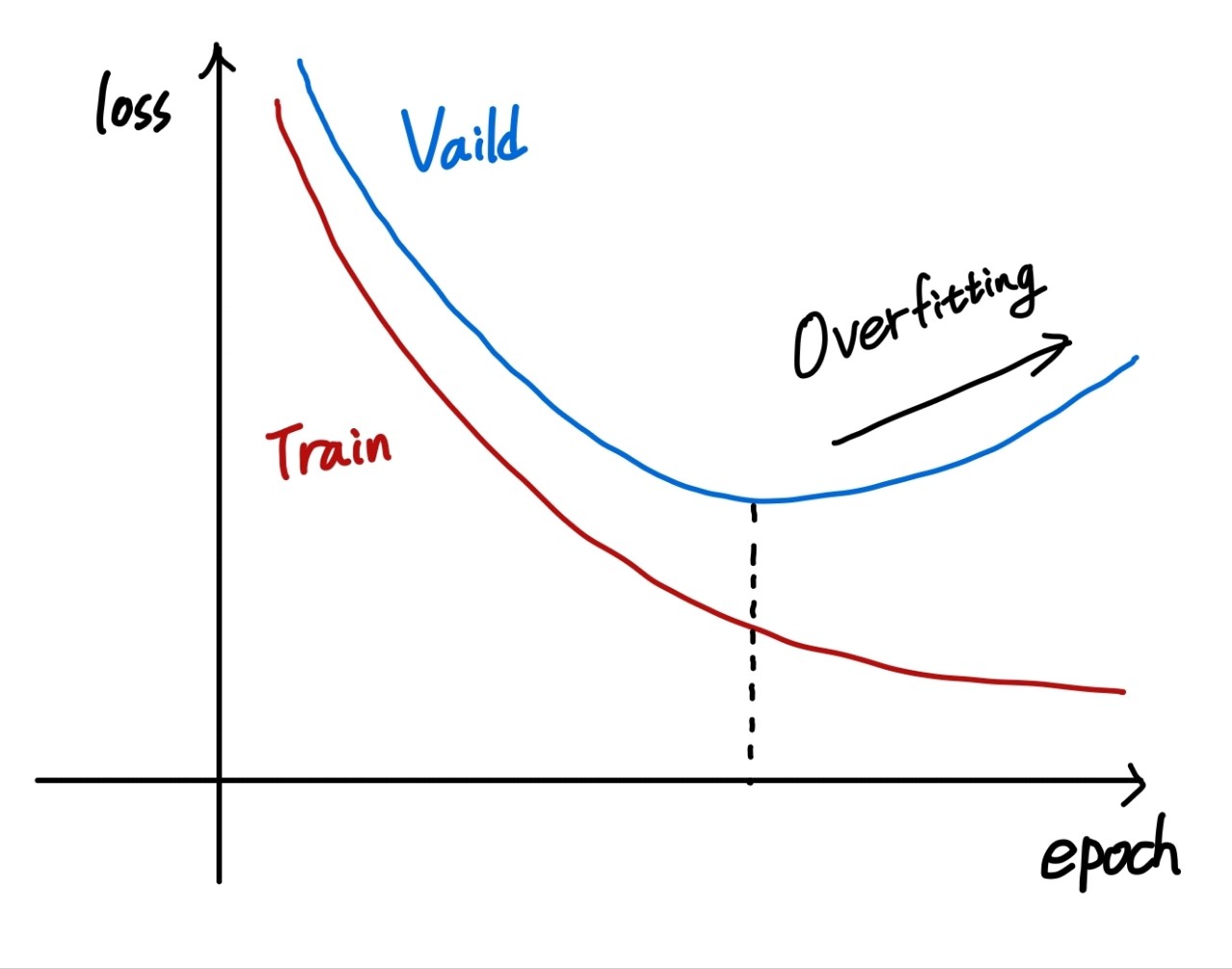
이러한 overfitting(과적합)을 막기 위해 test set과 vaild set을 사용하게 된다. 학습을 할 때 한 번도 보지 못했던 set을 이용하여 과적합 여부를 확인하는 것이다.
위와 같이 train set에 대한 loss는 감소하지만 valid set에 대한 loss가 감소하지 않을 때 과적합이 발생한다고 판단할 수 있다.
Regularization
과적합을 막기 위한 방법에는 더 많은 데이터를 사용한다거나, 더 적은 feature를 사용하는 방법 등 여러 방법이 있고, 그 중 하나가 regularization이다.
Regularization에는 다음과 같은 방법들이 있다.
- Early Stoping: valid set의 loss가 줄어들지 않을 때 학습을 중지한다.
- Reducing Network Size
- Weight Decay: weight가 너무 커지지 않도록 wight가 커질수록 함께 커지는 penalty를 부여한다.
- Dropout: node의 일부를 꺼서 학습하는 node를 줄인다.
- Batch Normalization: 학습 중에 배치 단위로 정규화 하는 것
with Code
Import
1
2
3
4
5
6
7
import torch
import torch.nn as nn
import torch.nn.functional as F
import torch.optim as optim
# 시드 고정
torch.manual_seed(1)
Data
3차원의 input과 3개의 class를 가지고 있는 label로 학습을 진행하며, train set과 test set의 비율은 8:3이다.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
# train set
x_train = torch.FloatTensor([[1, 2, 1],
[1, 3, 2],
[1, 3, 4],
[1, 5, 5],
[1, 7, 5],
[1, 2, 5],
[1, 6, 6],
[1, 7, 7]
])
y_train = torch.LongTensor([2, 2, 2, 1, 1, 1, 0, 0])
# test set
x_test = torch.FloatTensor([[2, 1, 1], [3, 1, 2], [3, 3, 4]])
y_test = torch.LongTensor([2, 2, 2])
Model
lab6에서 다뤘던 softamx model을 사용하여 학습을 진행한다.
물론 입출력 차원은 맞춰줘야 하기 때문에 self.linear = nn.Linear(3, 3)로 선형 모델을 정의하는 부분만 달라졌다.
1
2
3
4
5
6
7
8
class SoftmaxClassifierModel(nn.Module):
def __init__(self):
super().__init__()
self.linear = nn.Linear(3, 3)
def forward(self, x):
return self.linear(x)
model = SoftmaxClassifierModel()
Train
이 부분 역시 기존의 틀을 벗어나지 않는다.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
# optimizer 설정
optimizer = optim.SGD(model.parameters(), lr=0.1)
def train(model, optimizer, x_train, y_train):
nb_epochs = 20
for epoch in range(nb_epochs):
# H(x) 계산
prediction = model(x_train)
# cost 계산
cost = F.cross_entropy(prediction, y_train)
# cost로 H(x) 개선
optimizer.zero_grad()
cost.backward()
optimizer.step()
print('Epoch {:4d}/{} Cost: {:.6f}'.format(
epoch, nb_epochs, cost.item()
))
def test(model, optimizer, x_test, y_test):
prediction = model(x_test)
predicted_classes = prediction.max(1)[1]
correct_count = (predicted_classes == y_test).sum().item()
cost = F.cross_entropy(prediction, y_test)
print('Accuracy: {}% Cost: {:.6f}'.format(
correct_count / len(y_test) * 100, cost.item()
))
train(model, optimizer, x_train, y_train)
test(model, optimizer, x_test, y_test)
'''output
Epoch 0/20 Cost: 2.203667
Epoch 1/20 Cost: 1.199645
Epoch 2/20 Cost: 1.142985
Epoch 3/20 Cost: 1.117769
Epoch 4/20 Cost: 1.100901
Epoch 5/20 Cost: 1.089523
Epoch 6/20 Cost: 1.079872
Epoch 7/20 Cost: 1.071320
Epoch 8/20 Cost: 1.063325
Epoch 9/20 Cost: 1.055720
Epoch 10/20 Cost: 1.048378
Epoch 11/20 Cost: 1.041245
Epoch 12/20 Cost: 1.034285
Epoch 13/20 Cost: 1.027478
Epoch 14/20 Cost: 1.020813
Epoch 15/20 Cost: 1.014279
Epoch 16/20 Cost: 1.007872
Epoch 17/20 Cost: 1.001586
Epoch 18/20 Cost: 0.995419
Epoch 19/20 Cost: 0.989365
Accuracy: 0.0% Cost: 1.425844
'''
임의로 넣은 값들이라 예측의 의미는 크게 없어 보인다. 모델을 어떻게 학습하는지에 대한 코드만 참고하면 될 것 같다.
Learning Rate
\[ W := W - \alpha \nabla W \,\,\left(\alpha = learning\,\,rate\right)\]
위와 같은 gradient descent 식에서 $\alpha$가 learning rate(학습률)이다. 학습하는 비율이라고 간단하게 언급하고 넘어갔었는데, 이번에는 어떤 영향을 미치는지 확인해 보자.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
model = SoftmaxClassifierModel()
optimizer = optim.SGD(model.parameters(), lr=1e5)
train(model, optimizer, x_train, y_train)
'''output
Epoch 0/20 Cost: 1.280268
Epoch 1/20 Cost: 976950.812500
Epoch 2/20 Cost: 1279135.125000
Epoch 3/20 Cost: 1198379.000000
Epoch 4/20 Cost: 1098825.875000
Epoch 5/20 Cost: 1968197.625000
Epoch 6/20 Cost: 284763.250000
Epoch 7/20 Cost: 1532260.125000
Epoch 8/20 Cost: 1651504.000000
Epoch 9/20 Cost: 521878.500000
Epoch 10/20 Cost: 1397263.250000
Epoch 11/20 Cost: 750986.250000
Epoch 12/20 Cost: 918691.500000
Epoch 13/20 Cost: 1487888.250000
Epoch 14/20 Cost: 1582260.125000
Epoch 15/20 Cost: 685818.062500
Epoch 16/20 Cost: 1140048.750000
Epoch 17/20 Cost: 940566.500000
Epoch 18/20 Cost: 931638.250000
Epoch 19/20 Cost: 1971322.625000
'''
학습률이 너무 큰 경우이다. 학습률이 크면 한번에 학습하려는 정도가 커지는데 이 정도가 너무 크게 되면, 점점 gradient가 커지면서 발산(overshooting)하게 된다.
위 코드의 결과를 보면 cost가 학습할 수록 커지고 있는 것을 확인할 수 있다.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
model = SoftmaxClassifierModel()
optimizer = optim.SGD(model.parameters(), lr=1e-10)
train(model, optimizer, x_train, y_train)
'''output
Epoch 0/20 Cost: 3.187324
Epoch 1/20 Cost: 3.187324
Epoch 2/20 Cost: 3.187324
Epoch 3/20 Cost: 3.187324
Epoch 4/20 Cost: 3.187324
Epoch 5/20 Cost: 3.187324
Epoch 6/20 Cost: 3.187324
Epoch 7/20 Cost: 3.187324
Epoch 8/20 Cost: 3.187324
Epoch 9/20 Cost: 3.187324
Epoch 10/20 Cost: 3.187324
Epoch 11/20 Cost: 3.187324
Epoch 12/20 Cost: 3.187324
Epoch 13/20 Cost: 3.187324
Epoch 14/20 Cost: 3.187324
Epoch 15/20 Cost: 3.187324
Epoch 16/20 Cost: 3.187324
Epoch 17/20 Cost: 3.187324
Epoch 18/20 Cost: 3.187324
Epoch 19/20 Cost: 3.187324
'''
이번에는 학습률이 너무 작은 경우이다. 이 때는 발산할 확률은 거의 없겠지만 학습이 너무 느리거나 진행이 되지 않는다.
위 코드에서 보면 cost가 변하지 않는 것을 확인할 수 있다.
그래서 적절한 학습률을 찾기 위해서는 발산하면 작게, cost가 줄어들지 않으면 크게 조정하는 것이 바람직하다.
Data Preprocessing
학습이 잘 될 수 있도록 data를 학습 전에 처리해 주는 것을 Data Preprocessing(데이터 전처리)이라고 한다.
Standardization
이런 전처리 중 하나인 Standardization(정규화)을 한번 알아보자. 정규화의 식은 다음과 같이 주어진다.
\[ x’_j = \frac{x_j - \mu_j}{\sigma_j} \]
여기서 $\sigma$는 표준 분산, $\mu$는 평균을 의미한다. 이들을 코드로 표현하면 다음과 같다.
1
2
3
4
5
6
7
8
9
10
11
12
13
mu = x_train.mean(dim=0)
sigma = x_train.std(dim=0)
norm_x_train = (x_train - mu) / sigma
print(norm_x_train)
'''output
tensor([[-1.0674, -0.3758, -0.8398],
[ 0.7418, 0.2778, 0.5863],
[ 0.3799, 0.5229, 0.3486],
[ 1.0132, 1.0948, 1.1409],
[-1.0674, -1.5197, -1.2360]])
'''
이걸 이용해서 training을 하려면 다음과 같은 결과가 나온다.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
train(model, optimizer, norm_x_train, y_train)
'''output
Epoch 0/20 Cost: 29785.091797
Epoch 1/20 Cost: 18906.164062
Epoch 2/20 Cost: 12054.674805
Epoch 3/20 Cost: 7702.029297
Epoch 4/20 Cost: 4925.733398
Epoch 5/20 Cost: 3151.632568
Epoch 6/20 Cost: 2016.996094
Epoch 7/20 Cost: 1291.051270
Epoch 8/20 Cost: 826.505310
Epoch 9/20 Cost: 529.207336
Epoch 10/20 Cost: 338.934204
Epoch 11/20 Cost: 217.153549
Epoch 12/20 Cost: 139.206741
Epoch 13/20 Cost: 89.313782
Epoch 14/20 Cost: 57.375462
Epoch 15/20 Cost: 36.928429
Epoch 16/20 Cost: 23.835772
Epoch 17/20 Cost: 15.450428
Epoch 18/20 Cost: 10.077808
Epoch 19/20 Cost: 6.633700
'''
정규화가 하려는 학습에 정말 좋은지는 학습하여 결과를 확인하는 것이 가장 좋겠지만, 이론적으로 분석을 하면 data 차원 간의 값의 차이가 크다거나 할 때 진행하면 좋은 효과를 볼 수 있다.
1
2
3
4
5
6
7
8
9
y = torch.FloatTensor([[0.0011, 2000, 1],
[0.001, 3000, 2],
[0.0001, 3000, 4],
[0.0021, 5000, 5],
[0.0131, 7000, 5],
[0.0211, 2000, 5],
[0.1211, 6000, 6],
[0.0001, 7000, 7]
])
예를 들어 위와 같은 target이 있다. 이 데이터의 값을 차원별로 비교해 보면, 그 차이가 너무 큰 것을 볼 수 있다. 이렇게 되어버리면 2번째 값(1000 단위)에 대한 loss를 최소화 하는 것이 훨씬 이득이라고 생각하여 다른 값들에 대한 학습이 제대로 되지 않을 수 있다.
이때 정규화를 통해 적절한 범위로 값을 잡아주면 모든 데이터들이 균등하게 학습이 될 수 있다.