Post

모두를 위한 딥러닝 2 - Lab9-4:Batch Normalization

Posted Updated
By
6 min read
모두를 위한 딥러닝 2 - Lab9-4:Batch Normalization

모두를 위한 딥러닝 Lab9-4: Batch Normalization 강의를 본 후 공부를 목적으로 작성한 게시물입니다.

Gradient Vanishing / Gradient Exploding

Gradient Vanishing(기울기 소실)과 Gradient Exploding(기울기 폭주)는 정상적인 학습을 할 수 없게 만드는 요인들이다.

기울기 소실은 앞서 살펴본 것처럼 역전파를 수행할 때 작은 미분값을 chain rule에 따라 계속 곱하다가 결국 0으로 소멸해버리는 것이었다.

반대로 기울기 폭주는 너무 큰 미분값을 계속 곱하다가 수렴하지 못하고 발산해버리는 것을 의미한다.

이들을 방지하기 위해 시도해볼 수 있는 것은 아래와 같은 방법들이 있다

  • Change activation function
  • Careful initialization
  • Small learning rate
  • Batch Normalization

이 중에서 이번 강의에서는 Batch Normalization에 대한 내용을 다루었다.

Batch normalization을 제시할 때 주장했던 기울기 소실과 폭주에 대한 주된 이유가 Internal Covariate Shift였는데 이에 대해 한번 알아보자.

Covariate Shift

먼저 Covariate Shift는 공변량 변화라고도 하는데 입력 데이터의 분포가 학습할 때와 테스트할 때 다르게 나타나는 현상을 말한다.

예를 들어 손글씨를 분류하는 모델을 만드려고 할 때 학습 데이터로 한글 손글씨를 사용해서 학습한 후 영어 손글씨를 분류하려고 하면 당연히 분류가 제대로 되지 않을 것이다.

이는 모델이 학습한 분포와 테스트 데이터의 분포가 다르기 때문이다.

Internal Covariate Shift

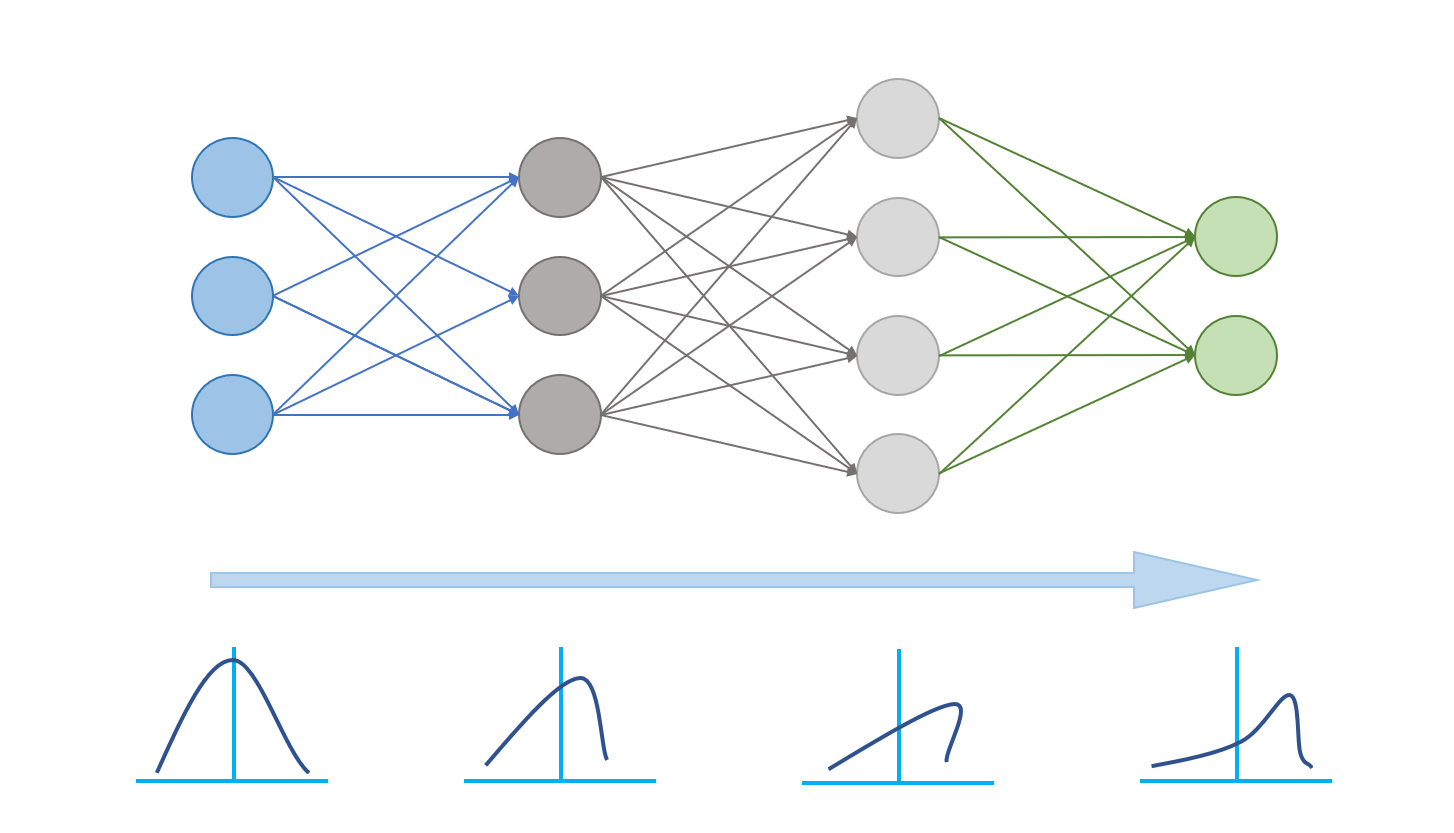
이런 Covariate Shift가 네트워크 내부에서 발생하는 것이 Inteanal Covariate Shift이다.

이전까지는 모델 단위의 분포 문제라고 생각하고 첫 입력에만 normalization을 했지만, 실제로는 아래와 같이 스탭마다 레이어 단위로 Covariate Shift가 발생한다는 것이다.

Internal Covariate Shift

그러므로 각 레이어 학습마다 각 minibatch를 normalization을 해야 하며 이를 Batch normalization이라고 한다.

Batch Normalization

Batch normalization은 다음과 같은 알고리즘으로 진행된다.

Batch Normalization Algorithm

$\mu_\mathcal{B}$와 $\sigma^2_\mathcal{B}$는 minibatch를 통해 게산된 평균과 분산이며 sample mean/variance라고도 불린다. 이들을 이용해서 normalize 하게 되는데 이때 $\epsilon$은 0으로 나누는 것을 방지하는 아주 작은 값이다.

이렇게 normalize된 데이터를 가지고 $\gamma$와 $\beta$를 학습하면 Batch normalization을 통한 학습이 한 번 끝나게 된다.

Evaluation

검증할 때 Batch normalization을 사용하는 모델이 값의 일부가 바뀐 batch를 받는다면 그 batch의 $\mu_\mathcal{B}$와 $\sigma^2_\mathcal{B}$ 역시 바뀌게 된다. 이렇게 되면 $\hat{x}$도 다르게 계산되는데 이럴 경우 같은 값이라도 batch의 일부분이 바뀌었다는 사실 하나만으로 다른 결과가 나오게 된다.

검증 과정에서 이러한 일일 발생하는 것을 막기 위해 학습 시에 게산했던 $\mu_\mathcal{B}$와 $\sigma^2\mathcal{B}$를 따로 저장해 두고, test할 때는 이미 계산된 $\mu\mathcal{B}$와 $\sigma^2_\mathcal{B}$를 사용한다.

이런 방식으로 결과값을 도출하면 같은 값에 같은 결과를 얻을 수 있다. 이런 이유로 Batch normalization도 dropout과 같이 따로 eval mode로 바꿔줘야 한다.

Train

Batch normalization을 적용하려면 기존 코드에서 torch.nn.BatchNorm1d를 추가하여 model을 구성하면 된다. 위치는 activation 직전에 사용하는 것이 일반적이라고 한다.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26

# nn layers
linear1 = torch.nn.Linear(784, 32, bias=True)
linear2 = torch.nn.Linear(32, 32, bias=True)
linear3 = torch.nn.Linear(32, 10, bias=True)
relu = torch.nn.ReLU()
bn1 = torch.nn.BatchNorm1d(32)
bn2 = torch.nn.BatchNorm1d(32)

nn_linear1 = torch.nn.Linear(784, 32, bias=True)
nn_linear2 = torch.nn.Linear(32, 32, bias=True)
nn_linear3 = torch.nn.Linear(32, 10, bias=True)

# model with Batch normalization
bn_model = torch.nn.Sequential(linear1, bn1, relu,
                            linear2, bn2, relu,
                            linear3).to(device)

# model without Batch normalization
nn_model = torch.nn.Sequential(nn_linear1, relu,
                               nn_linear2, relu,
                               nn_linear3).to(device)

# define cost/loss & optimizer
criterion = torch.nn.CrossEntropyLoss().to(device)    # Softmax is internally computed.
bn_optimizer = torch.optim.Adam(bn_model.parameters(), lr=learning_rate)
nn_optimizer = torch.optim.Adam(nn_model.parameters(), lr=learning_rate)

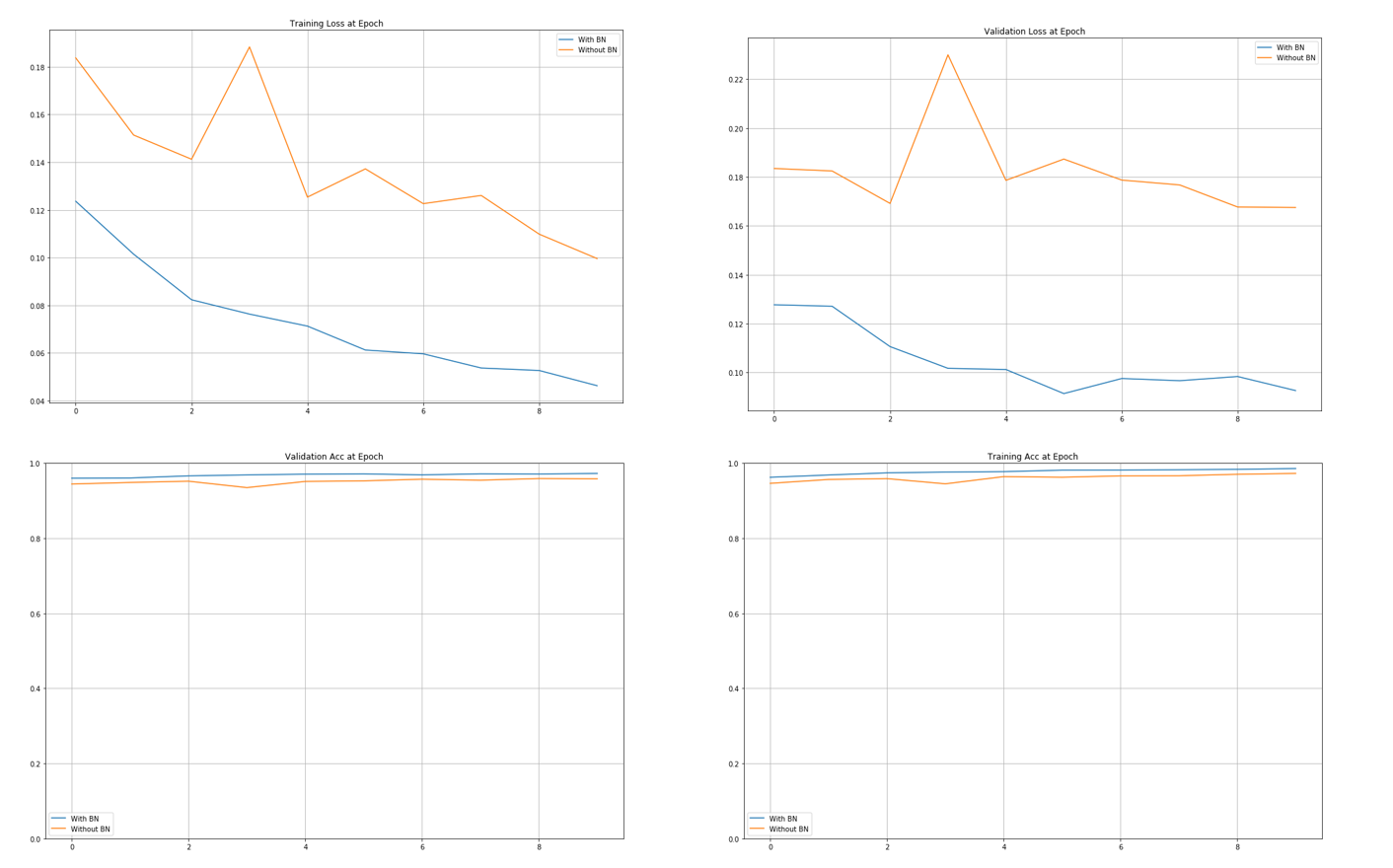
model은 위에서 말한 것처럼 이와같이 구현할 수 있고, 학습은 dropout과 동일하게 model.train()을 먼저 해 주고 진행하면 된다.

실제로 Batch normalization을 적용한 경우가 더 학습이 잘 된것을 확인할 수 있다.

Image Source

pytorch, study
batch-normalization gradient-vanishing gradient-exploding internal-covariate-shift
This post is licensed under CC BY 4.0 by the author.