모두를 위한 딥러닝 2 - Lab6: Softmax Classification
모두를 위한 딥러닝 Lab 6: Softmax Classification 강의를 본 후 공부를 목적으로 작성한 게시물입니다.
Softmax Classification(Multinomial Classification)
이전 포스팅에서는 이진 분류 문제에 대해 알아봤다. 이번에는 분류해야 할 범주가 2개(0, 1)가 아니라 여러개인 다중 분류에 대해 알아보려 한다.
Hypothesis
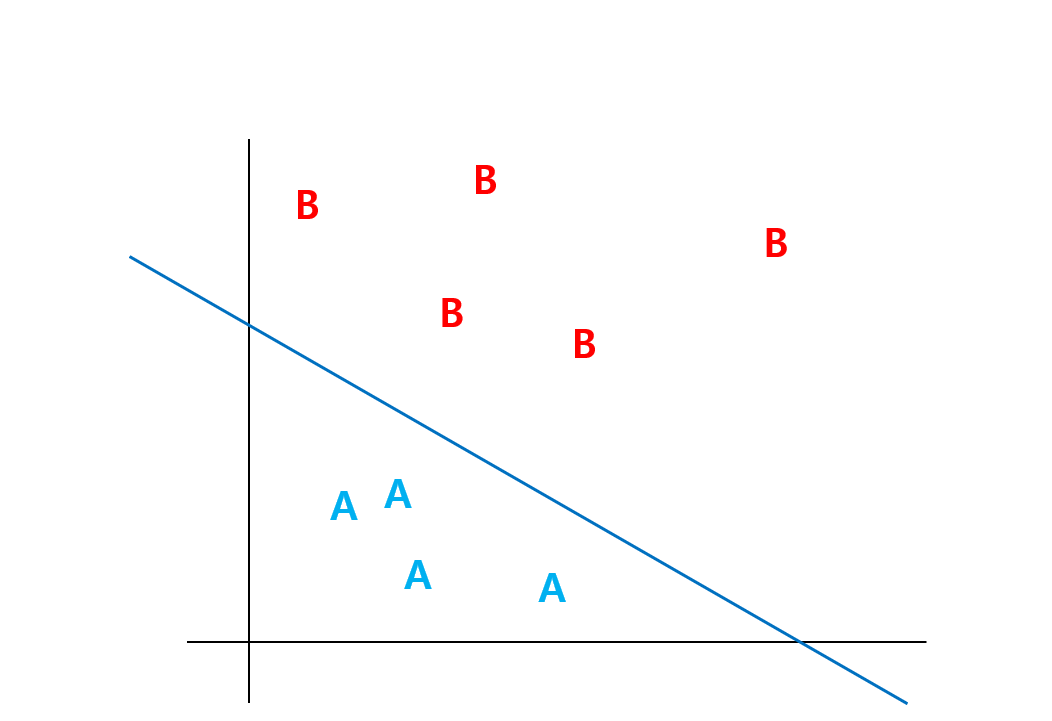
이진 분류는 다음과 같이 두 카테고리의 값들이 잘 나눠질 수 있는 선을 긋는 것과 같다.
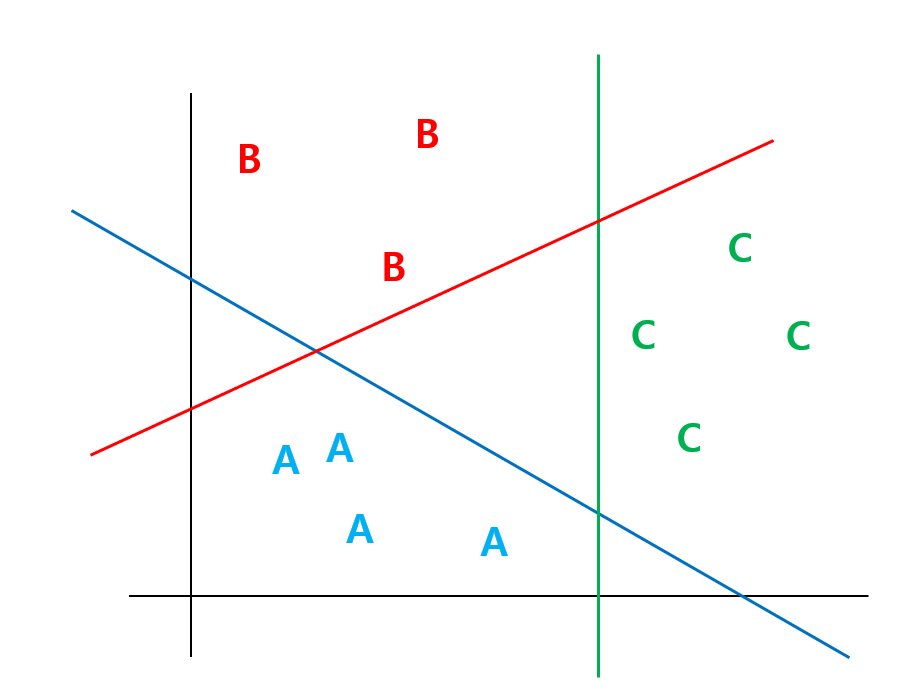
이처럼 다중 분류도 여러 카테고리의 값들을 잘 나누는 선들을 긋는다고 생각해 보자. 그러면 다음과 같은 그림이 그려질 것이다.
파란색 선은 A or not, 빨간색 선은 B or not 그리고 초록색 선은 C or not으로 구분하고 있다고 생각하면 각 카테고리마다 하나의 분류 문제로 볼 수 있다.
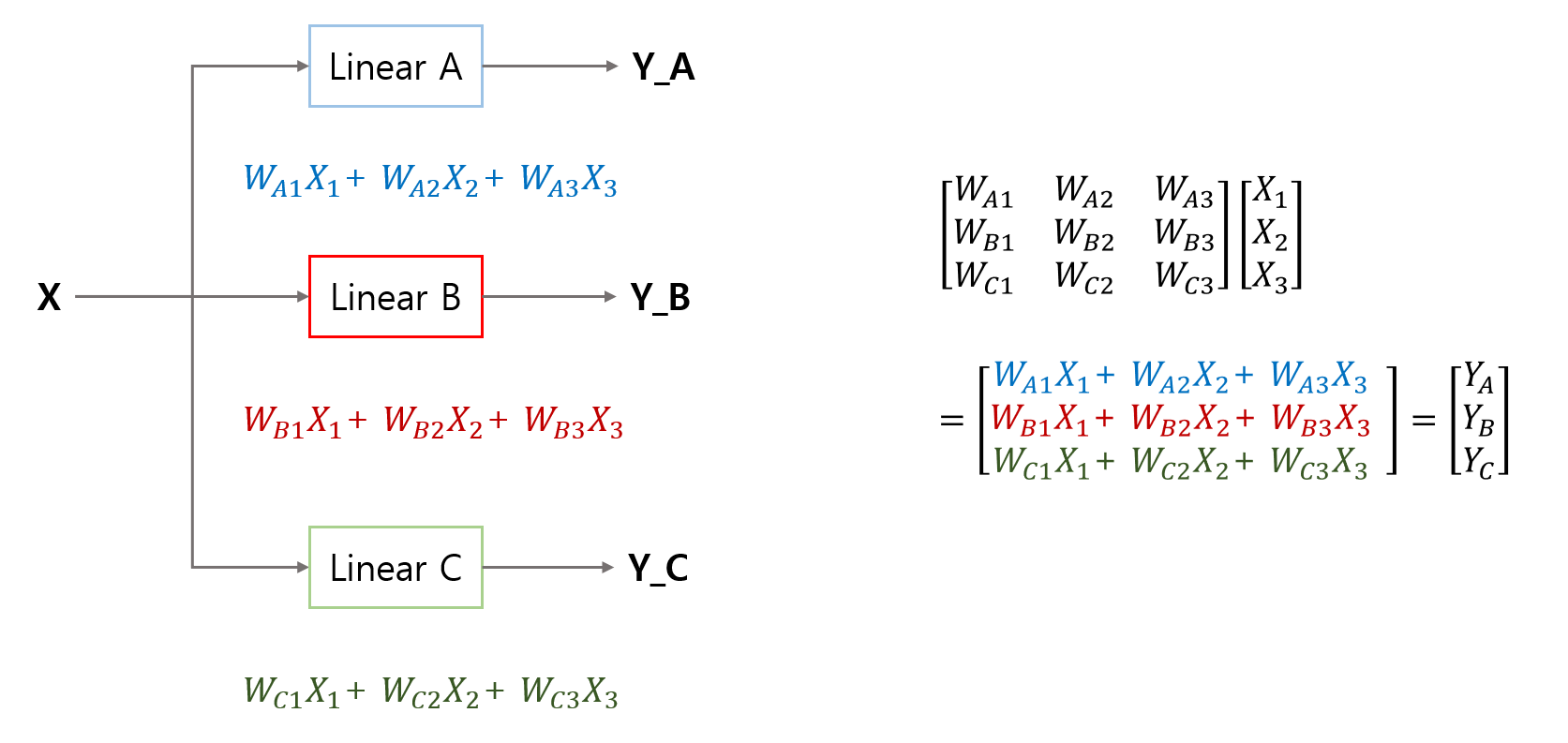
이 말은 각각의 카테고리를 분류하는 hypothesis를 정의할 수 있다는 것인데, 이를 다음과 같이 행렬의 연산으로 깔끔하게 나타낼 수 있다.
이렇게 나온 확률을 각각 시그모이드로 처리하여 값을 낼 수도 있겠지만, 이때 조금 더 편하고 최적화된 함수로 softmax를 사용하게 되며 다음과 같이 정의된다.
\[ P(class=i) = \frac{e^i}{\sum e^i} \]
max를 soft하게 뽑는 것으로, 이 값이 최대인가, 아닌가로 단정지어 출력하는 것이 아니라 최대일 확률을 출력하는 거라고 이해하면 될것 같다.
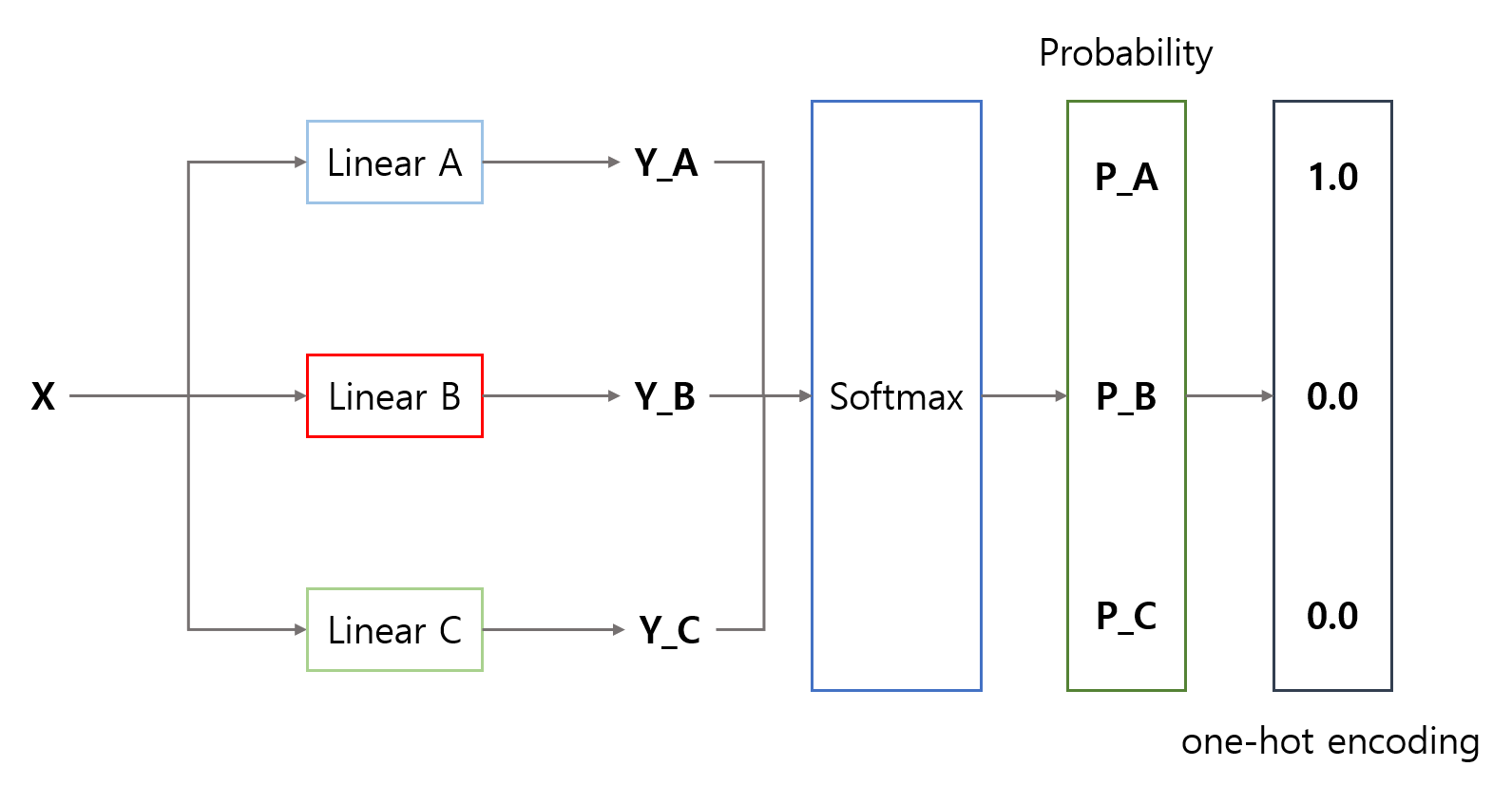
이렇게 뽑은 확률값으로 원-핫 인코딩하여 최종적으로 어느 카테고리에 속하는지 출력하게 된다. 아래 그림은 A 카테고리에 속한다고 생각할 때의 출력을 보인 것이다.
코드로는 torch에서 제공하는 함수를 사용하면 된다.
1
2
3
4
5
6
7
8
9
10
import torch
import torch.nn.functional as F
z = torch.FloatTensor([1, 2, 3])
hypothesis = F.softmax(z, dim=0)
print(hypothesis)
'''output
tensor([0.0900, 0.2447, 0.6652])
'''
가장 큰 값인 3의 확률이 가장 크게(softmax) 출력된 것을 확인할 수 있다.
Cost(Cross Entropy)
hHypothesis까지 모두 정의했으니, 이제 그에 맞는 cost를 정의해야 한다. 다중 분류에서는 cross entropy를 cost로 사용하는데, 이는 간단히 말해서 예측한 확률이 실제 분포의 확률과 얼마나 차이가 나는지 계산한 값이다.
자세한 내용은 이미 cross entropy 포스팅에서 다루었기 때문에 여기로 돌리고 바로 코드로 넘아가자. 실제 값을 원핫 인코딩 한 것에, softmax에 log를 취한 값을 원소별로 곱한 뒤에, 0이 아닌 값들은 평균내어 전체적인 cross entropy를 구할 수 있다.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
z = torch.rand(3, 5, requires_grad=True)
hypothesis = F.softmax(z, dim=1)
print(hypothesis)
y = torch.randint(5, (3,)).long()
print(y)
y_one_hot = torch.zeros_like(hypothesis)
y_one_hot.scatter_(1, y.unsqueeze(1), 1)
cost = (y_one_hot * -torch.log(hypothesis)).sum(dim=1).mean()
print(cost)
'''output
tensor([[0.2645, 0.1639, 0.1855, 0.2585, 0.1277],
[0.2430, 0.1624, 0.2322, 0.1930, 0.1694],
[0.2226, 0.1986, 0.2326, 0.1594, 0.1868]], grad_fn=<SoftmaxBackward0>)
tensor([0, 2, 1])
tensor([[1., 0., 0., 0., 0.],
[0., 0., 1., 0., 0.],
[0., 1., 0., 0., 0.]])
tensor(1.4689, grad_fn=<MeanBackward0>)
'''
아니면 softmax처럼 미리 구현되어 있는 것을 사용해도 된다.
```python
# -log를 취해서 평균내는 것까지만 torch 함수 사용 (Negative Log Likelihood)
F.nll_loss(F.log_softmax(z, dim=1), y)
# NLL과 softmax를 묶어 torch 함수로 사용
F.cross_entropy(z, y)
Training data
4차원의 input, 3가지의 class를 답으로 가진 데이터 셋이다.
1
2
3
4
5
6
7
8
9
10
11
x_train = [[1, 2, 1, 1],
[2, 1, 3, 2],
[3, 1, 3, 4],
[4, 1, 5, 5],
[1, 7, 5, 5],
[1, 2, 5, 6],
[1, 6, 6, 6],
[1, 7, 7, 7]]
y_train = [2, 2, 2, 1, 1, 1, 0, 0]
x_train = torch.FloatTensor(x_train)
y_train = torch.LongTensor(y_train)
Train
Hypothesis와 cost이외에는 크게 달라진 점은 없다. 3가지 방식의 구현 코드만 한번 살펴보자
F.softmax + torch.log
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
W = torch.zeros((4, 3), requires_grad=True)
b = torch.zeros(1, requires_grad=True)
optimizer = optim.SGD([W, b], lr=0.1)
nb_epochs = 1000
for epoch in range(nb_epochs + 1):
hypothesis = F.softmax(x_train.matmul(W) + b, dim=1)
y_one_hot = torch.zeros_like(hypothesis)
y_one_hot.scatter_(1, y_train.unsqueeze(1), 1)
cost = (y_one_hot * -torch.log(hypothesis)).sum(dim=1).mean()
optimizer.zero_grad()
cost.backward()
optimizer.step()
# 100번마다 로그 출력
if epoch % 100 == 0:
print('Epoch {:4d}/{} Cost: {:.6f}'.format(
epoch, nb_epochs, cost.item()
))
'''output
Epoch 0/1000 Cost: 1.098612
Epoch 100/1000 Cost: 0.761050
Epoch 200/1000 Cost: 0.689991
Epoch 300/1000 Cost: 0.643229
Epoch 400/1000 Cost: 0.604117
Epoch 500/1000 Cost: 0.568255
Epoch 600/1000 Cost: 0.533922
Epoch 700/1000 Cost: 0.500291
Epoch 800/1000 Cost: 0.466908
Epoch 900/1000 Cost: 0.433507
Epoch 1000/1000 Cost: 0.399962
'''
F.cross_entropy
softmax가 cross entropy에 속해 있기 때문에 hypothesis에는 softmax가 없는 모습을 볼 수 있다.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
W = torch.zeros((4, 3), requires_grad=True)
b = torch.zeros(1, requires_grad=True)
optimizer = optim.SGD([W, b], lr=0.1)
nb_epochs = 1000
for epoch in range(nb_epochs + 1):
z = x_train.matmul(W) + b
cost = F.cross_entropy(z, y_train)
optimizer.zero_grad()
cost.backward()
optimizer.step()
if epoch % 100 == 0:
print('Epoch {:4d}/{} Cost: {:.6f}'.format(
epoch, nb_epochs, cost.item()
))
nn.Module
class를 정의하여 사용할 수도 있다.
1
2
3
4
5
6
7
class SoftmaxClassifierModel(nn.Module):
def __init__(self):
super().__init__()
self.linear = nn.Linear(4, 3) # Output이 3!
def forward(self, x):
return self.linear(x)
이때도 마찬가지로 softmax가 cross entropy에 속해 있기 때문에 class를 정의할 때는 선형 함수 부분만 정의해 준 것을 볼 수 있다.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
model = SoftmaxClassifierModel()
optimizer = optim.SGD(model.parameters(), lr=0.1)
nb_epochs = 1000
for epoch in range(nb_epochs + 1):
prediction = model(x_train)
cost = F.cross_entropy(prediction, y_train)
optimizer.zero_grad()
cost.backward()
optimizer.step()
if epoch % 100 == 0:
print('Epoch {:4d}/{} Cost: {:.6f}'.format(
epoch, nb_epochs, cost.item()
))