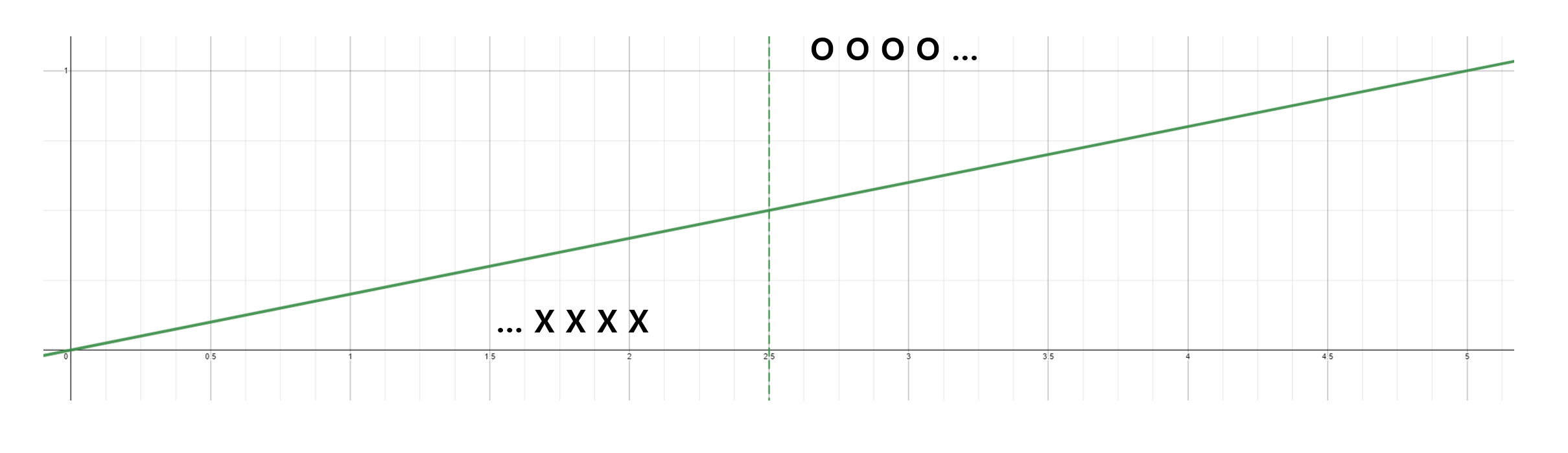모두를 위한 딥러닝 2 - Lab5: Logistic Classification
모두를 위한 딥러닝 Lab 5: Logistic Classification 강의를 본 후 공부를 목적으로 작성한 게시물입니다.
Logistic Regression(Binary Classification)
Hypothesis로 sigmoid(logistic) 함수를 사용하는 회귀 방법이다. 흔히 Binary classification ploblem에 많이 사용하는데, 이 경우 왜 선형 회귀 대신 로지스틱 회귀를 사용하는지에 대해 먼저 알아보자
Hypothesis
공부 시간에 따른 시험 합격 여부 데이터 셋을 생각해 보자($y=1$: 합격, $y=0$: 불합격).
먼저 이 데이터 셋의 예측 문제를 선형 회귀를 통해 접근해 볼 것이다. 기존의 선형 회귀식의 hypothesis는 $H(x_1, x_2, x_3) = xw + b$로 주어졌었다. 학습 초기에는 2.5시간(초록색 점선)을 기준으로 합격이 결정되었다고 가정해 보자
위와 같이 회귀 함수를 학습하면 x(공부 시간)가 주어졌을 때 y가 0.5를 넘었는가 여부에 따라 분류가 가능할 것이다(0.5를 넘으면 합격으로 처리하면 된다).
하지만 이 회귀식의 범위를 넘어서는 값 즉, 학습된 hypothesis에 넣었을 때 prediction이 $[0, 1]$를 벗어나는 값이 있다면 그에 맞춰 회귀선을 다시 학습해야 한다.
위처럼 9시간(빨간 O) 공부한 사람에 맞춰 학습을 다시 하면 2.5시간에서 5시간 사이의 범위에 있는 사람들은 모델이 불합격한 것으로 판단하게 된다.
이런 상황과 같이 적절한 분류를 하기 힘든 경우가 실제 데이터에서는 무수히 많이 존재할 수 있고, 학습이 끝난 이후 예측을 할 때 prediction의 범위가 $[0, 1]$을 벗어날 수 있다는 문제도 있다. 이러한 이유들로 선형 회귀만으로 접근하는 것은 분류 문제에는 적합하지 않다고 할 수 있다.
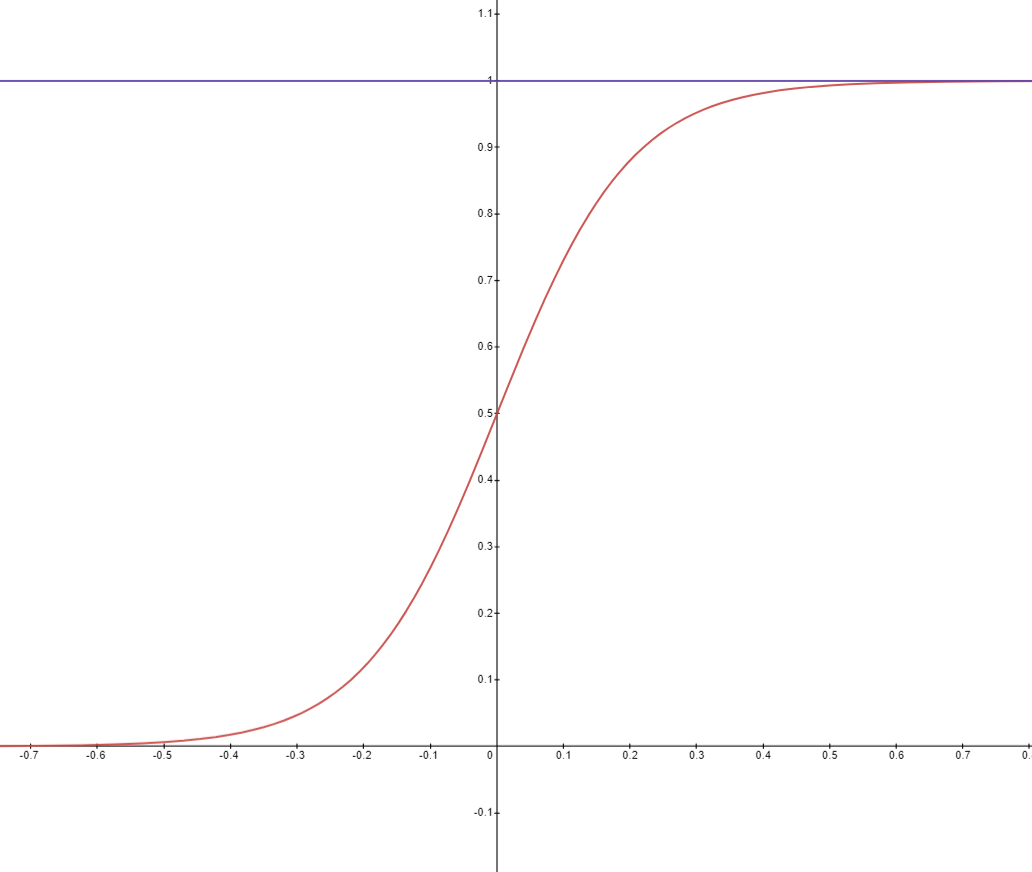
이번에는 로지스틱 회귀로 이 문제를 접근해 보자. 먼저 시그모이드 함수(로지스틱 함수)는 다음과 같이 정의된다.
\[ s(z) = \frac{1}{1+e^{-z}} \]
이를 그래프로 그려보면 아래와 같은 형태를 띈다.
그림으로도 확인할 수 있는 것처럼 시그모이드 함수는 항상 0과 1 사이에 값이 존재하여 앞서 언급한 선형 회귀의 문제점을 해결할 수 있다. 선형 회귀식을 시그모이드 함수의 인풋으로 넣으면 선형 회귀식에서 어떤 값이 나오든 0과 1사이의 범위를 넘어 생기는 문제가 일어나지 않을 것이다.
그러므로 로지스틱 회귀의 hypothesis는 로지스틱 함수에 선형 회귀식을 넣는 것으로 정의된다.
\[ H(X) = \frac{1}{1+e^{-W^T X}} \]
이 hypothesis를 따른다면 아무리 크거나 작은 값이 주어지더라도 0과 1사이를 벗어나지 않기 때문에 기존에 합격이라고 분류 된 값이 갑자기 불합격이 될 가능성이 매우 줄어든다.
이처럼 binary classification에 적합한 값으로 만들어 주는 특성 때문에 로지스틱 회귀 뿐만 아니라, neural network를 이용한 binary classification에서 output 직전의 마지막 레이어로도 사용된다. 이 때문에 activation function(활성화 함수)중 하나이기도 하다.
Cost(Binary Cross Entropy)
Hpothesis도 정의했으니 cost를 정의할 차례이다. 시그모이드 함수의 경우 선형 회귀에서 썼던 MSE를 사용하면 local minimun이 있을 수 있기 때문에 제대로 된 학습이 되지 않을 수 있다.
말로 하기보다 그래프로 한번 확인해 보자.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
import matplotlib.pyplot as plt
import torch
import numpy as np
import os
os.environ['KMP_DUPLICATE_LIB_OK']='True'
x_data = [[1, 2], [2, 3], [3, 1], [4, 3], [5, 3], [6, 2]]
y_data = [[0], [0], [0], [1], [1], [1]]
W_l = np.linspace(-3, 3, 1000)
cost_l = []
for W in W_l:
hypothesis = 1 / (1 + torch.exp(-(W * x_train)))
cost = torch.mean((hypothesis - y_train) ** 2)
cost_l.append(cost.item())
plt.plot(W_l, cost_l)
plt.xlabel('$W$')
plt.ylabel('Cost')
plt.show()
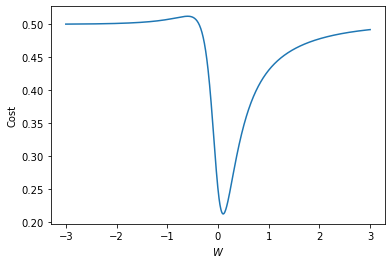
우리가 생각하기에 W가 0 근처의 값으로 수렴하는 것이 맞아 보인다. 하지만 gradient descent를 시작하는 점이 -1 부근, 혹은 더 작은 값이라면 우리가 원하는 방향과 반대로 극소점을 찾아갈 것이다. 그 방향에도 극소점이 있을 수 있겠지만 그건 우리가 원하는 global minimum이 아니다.
위 그래프는 조금 애매하다고 느낄 수 있겠지만 실제로 cost에 global minimum이 아닌 여러 극소점이 있다는 것은 확실히 학습이 잘 되지 않을 것이라는 건 알 수 있다.
그래서 cost로 다음과 같은 함수를 사용한다.
\[ cost(W) = -\frac{1}{m} \sum y \log\left(H(x)\right) + (1-y) \left( \log(1-H(x) \right) \]
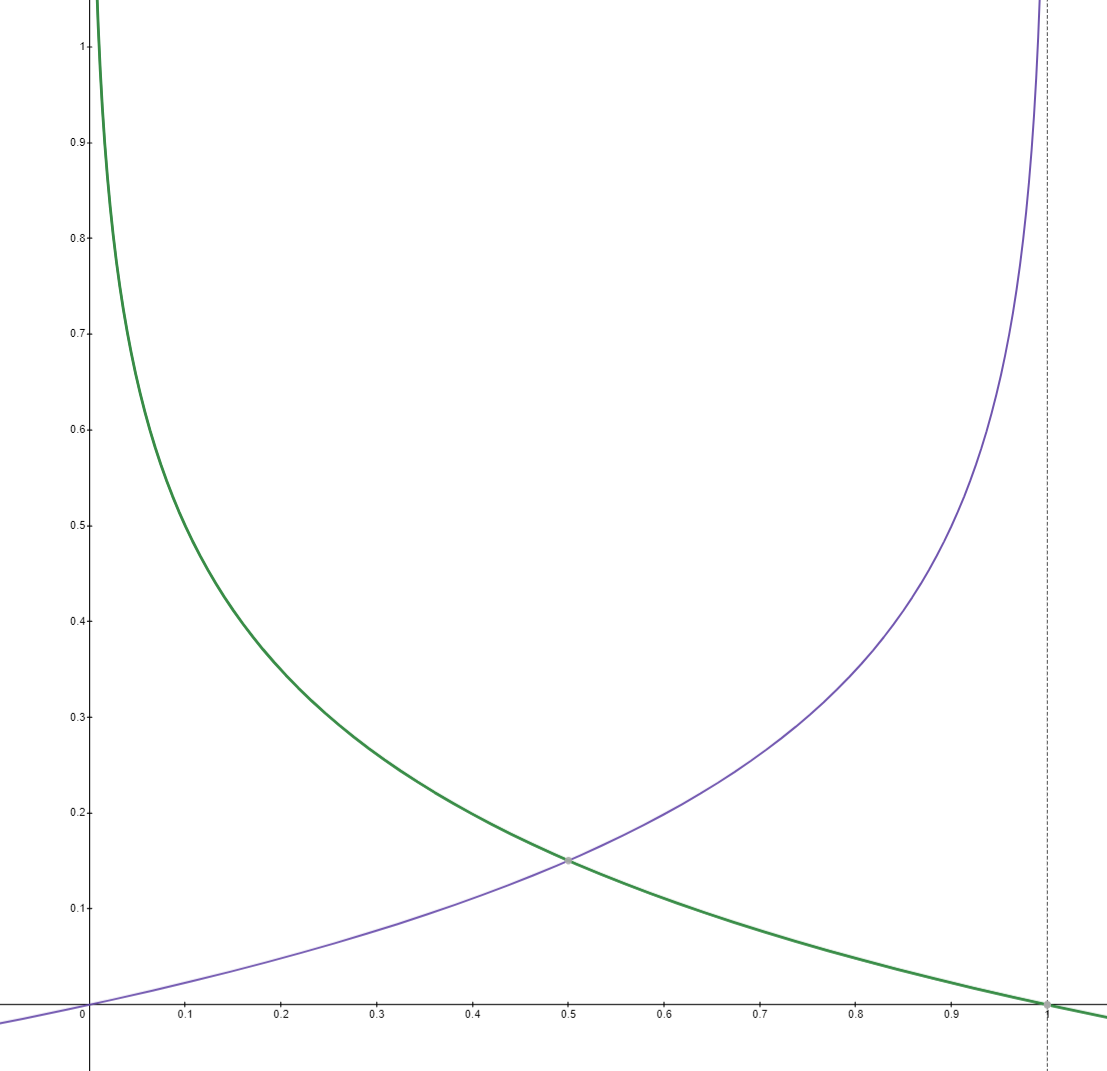
log를 사용하여 지수함수를 다루기 좋은 형태로 만들어 주고, 정답에 따라 적절한 cost를 사용할 수 있도록 만들었는데 그 cost의 형태는 다음과 같다.
답이 1인 경우(초록색) 0에 가까울 때 cost가 올라가고 1일 때 0이도록, 답이 0인 경우 그 반대로 작동하게 cost를 정의하였다. 덕분에 시그모이드를 이용해서 학습하기에 적절한 cost의 형태가 되었다.
이를 통한 gradient descent는 전과 동일한 형태로 진행한다.
\[ W := W - \alpha \frac{\partial}{\partial W} cost(W) \]
Import
1
2
3
4
5
6
7
import torch
import torch.nn as nn
import torch.nn.functional as F
import torch.optim as optim
# seed 고정
torch.manual_seed(1)
Training data
1
2
3
4
5
6
7
8
9
10
11
12
13
x_data = [[1, 2], [2, 3], [3, 1], [4, 3], [5, 3], [6, 2]]
y_data = [[0], [0], [0], [1], [1], [1]]
x_train = torch.FloatTensor(x_data)
y_train = torch.FloatTensor(y_data)
print(x_train.shape)
print(y_train.shape)
'''output
torch.Size([6, 2])
torch.Size([6, 1])
'''
Computing Hypothesis and Cost Function
일단은 수식 그대로 코드를 작성해서 사용해보자.
Hypothesis
\[ H(X) = \frac{1}{1+e^{-W^T X}} \]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
W = torch.zeros((2, 1), requires_grad=True)
b = torch.zeros(1, requires_grad=True)
hothesis = 1 / (1 + torch.exp(-(x_train.matmul(W) + b)))
print(hypothesis)
print(hypothesis.shape)
'''output
tensor([[0.5000],
[0.5000],
[0.5000],
[0.5000],
[0.5000],
[0.5000]], grad_fn=<MulBackward>)
torch.Size([6, 1])
'''
torch.exp(x)로 $e^x$연산을 할 수 있다. W와 b가 모두 0이기 때문에 0.5가 output으로 나온 것을 확인할 수 있다.
Cost
\[ cost(W) = -\frac{1}{m} \sum y \log\left(H(x)\right) + (1-y) \left( \log(1-H(x) \right) \]
1
2
3
4
5
6
7
8
9
10
11
losses = -(y_train * torch.log(hypothesis) + (1 - y_train) * torch.log(1 - hypothesis))
print(losses)
'''output
tensor([[0.6931],
[0.6931],
[0.6931],
[0.6931],
[0.6931],
[0.6931]], grad_fn=<NegBackward>)
'''
$log$ 연산도 마찬가지로 torch.log()를 통해 할 수 있다. loss도 잘 출력된다.
Full code
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
# 모델 초기화
W = torch.zeros((2, 1), requires_grad=True)
b = torch.zeros(1, requires_grad=True)
# optimizer 설정
optimizer = optim.SGD([W, b], lr=1)
nb_epochs = 1000
for epoch in range(nb_epochs + 1):
# Cost 계산
hypothesis = torch.sigmoid(x_train.matmul(W) + b) # or .mm or @
cost = -(y_train * torch.log(hypothesis) +
(1 - y_train) * torch.log(1 - hypothesis)).mean()
# cost로 H(x) 개선
optimizer.zero_grad()
cost.backward()
optimizer.step()
# 100번마다 로그 출력
if epoch % 100 == 0:
print('Epoch {:4d}/{} Cost: {:.6f}'.format(
epoch, nb_epochs, cost.item()
))
'''output
Epoch 0/1000 Cost: 0.693147
Epoch 100/1000 Cost: 0.134722
Epoch 200/1000 Cost: 0.080643
Epoch 300/1000 Cost: 0.057900
Epoch 400/1000 Cost: 0.045300
Epoch 500/1000 Cost: 0.037261
Epoch 600/1000 Cost: 0.031673
Epoch 700/1000 Cost: 0.027556
Epoch 800/1000 Cost: 0.024394
Epoch 900/1000 Cost: 0.021888
Epoch 1000/1000 Cost: 0.019852
'''
hypothesis와 cost가 달리진 것 외에는 이전의 lab들에서 학습하는 코드와 달라진 것이 없다.
Computing Hypothesis and Cost Function with torch
시그모이드 함수와 binary cross entropy는 PyTorch에서 기본적으로 제공하기 때문에 굳이 위처럼 구현하지 않고 사용할 수 있다
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
hypothesis = torch.sigmoid(x_train.matmul(W) + b)
print(hypothesis)
print(hypothesis.shape)
ptint(F.binary_cross_entropy(hypothesis, y_train))
'''output
tensor([[0.5000],
[0.5000],
[0.5000],
[0.5000],
[0.5000],
[0.5000]], grad_fn=<SigmoidBackward>)
torch.Size([6, 1])
tensor(0.6931, grad_fn=<BinaryCrossEntropyBackward>)
'''
앞서 수식으로 구현했던 것과 동일한 결과가 나온다.
Full Code
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
# 모델 초기화
W = torch.zeros((2, 1), requires_grad=True)
b = torch.zeros(1, requires_grad=True)
# optimizer 설정
optimizer = optim.SGD([W, b], lr=1)
nb_epochs = 1000
for epoch in range(nb_epochs + 1):
# Cost 계산
hypothesis = torch.sigmoid(x_train.matmul(W) + b) # or .mm or @
cost = F.binary_cross_entropy(hypothesis, y_train)
# cost로 H(x) 개선
optimizer.zero_grad()
cost.backward()
optimizer.step()
# 100번마다 로그 출력
if epoch % 100 == 0:
print('Epoch {:4d}/{} Cost: {:.6f}'.format(
epoch, nb_epochs, cost.item()
))
'''output
Epoch 0/1000 Cost: 0.693147
Epoch 100/1000 Cost: 0.134722
Epoch 200/1000 Cost: 0.080643
Epoch 300/1000 Cost: 0.057900
Epoch 400/1000 Cost: 0.045300
Epoch 500/1000 Cost: 0.037261
Epoch 600/1000 Cost: 0.031672
Epoch 700/1000 Cost: 0.027556
Epoch 800/1000 Cost: 0.024394
Epoch 900/1000 Cost: 0.021888
Epoch 1000/1000 Cost: 0.019852
'''
마잔가지로 hypothesis와 cost만 달라지고 기본적인 틀은 같다. 학습도 잘 되는 모습이다.
Evaluation
우리가 만든 모델이 얼마나 정확한지 확인해보자
실제 우리가 만든 모델은 시그모이드 함수의 결과값이기 때문에 다음과 같이 소수의 형태로 나타난다.
1
2
3
4
5
6
7
8
9
10
hypothesis = torch.sigmoid(x_train.matmul(W) + b)
print(hypothesis[:5])
'''output
tensor([[0.4103],
[0.9242],
[0.2300],
[0.9411],
[0.1772]], grad_fn=<SliceBackward>)
'''
실제로는 0또는 1의 값을 가지기 때문에 어떤 기준을 통해 결과값을 맞춰 줄 필요가 있어 보인다. 여기서는 0.5를 기준으로 0과 1을 나눈다고 생각하고 진행했다.
1
2
3
4
5
6
7
8
9
10
prediction = hypothesis >= torch.FloatTensor([0.5])
print(prediction[:5])
'''output
tensor([[0],
[1],
[0],
[1],
[0]], dtype=torch.uint8)
'''
이렇게 하면 0.5 이상의 값은 1로, 미만의 값는 0으로 맵핑하여 ByteTensor의 형태로 돌려준다.
실제 값과 비교해 보면 잘 예측한 것을 확인할 수 있다.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
print(prediction[:5])
print(y_train[:5])
correct_prediction = prediction.float() == y_train
print(correct_prediction[:5])
'''output
tensor([[0],
[1],
[0],
[1],
[0]], dtype=torch.uint8)
tensor([[0.],
[1.],
[0.],
[1.],
[0.]])
tensor([[1],
[1],
[1],
[1],
[1]], dtype=torch.uint8)
'''
모델이 예측한 값이 실제와 같았을 때 1을 반환하도록 했을 때 모두 1이 나왔으므로 주어진 간단한 데이터 셋에 한해서는 잘 학습이 되었다고 할 수 있다.
Higher Implementation with Class
Bynary Classification 문제에서 Sigmoid Reggression을 사용하려고 할 때 lab4_1에서 나왔건 것처럼 Module을 사용하여 calss를 만들어 진행할 수 있다.
이번에 사용한 데이터 셋은 모두를 위한 딥러닝 코드와 함께 제공되는 당뇨병 데이터셋이며 8개 차원의 인폿과 당뇨병 여부에 따른 0, 1의 값으로 데이터가 구성되어 있다.
Loading Real Data
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
import numpy as np
xy = np.loadtxt('data-03-diabetes.csv', delimiter=',', dtype=np.float32)
x_data = xy[:, 0:-1]
y_data = xy[:, [-1]]
x_train = torch.FloatTensor(x_data)
y_train = torch.FloatTensor(y_data)
print(x_train[0:5])
print(y_train[0:5])
'''output
tensor([[-0.2941, 0.4874, 0.1803, -0.2929, 0.0000, 0.0015, -0.5312, -0.0333],
[-0.8824, -0.1457, 0.0820, -0.4141, 0.0000, -0.2072, -0.7669, -0.6667],
[-0.0588, 0.8392, 0.0492, 0.0000, 0.0000, -0.3055, -0.4927, -0.6333],
[-0.8824, -0.1055, 0.0820, -0.5354, -0.7778, -0.1624, -0.9240, 0.0000],
[ 0.0000, 0.3769, -0.3443, -0.2929, -0.6028, 0.2846, 0.8873, -0.6000]])
tensor([[0.],
[1.],
[0.],
[1.],
[0.]])
'''
Train with Class
차원에 맞춰 class를 정의해 준다. 이때 바로 시그모이드 함수에 넣는 것이 아니라 linear function으로 만들어 준 후에 적용해야 우리가 원하는 hypothesis가 만들어진다.
1
2
3
4
5
6
7
8
class BinaryClassifier(nn.Module):
def __init__(self):
super().__init__()
self.linear = nn.Linear(8, 1)
self.sigmoid = nn.Sigmoid()
def forward(self, x):
return self.sigmoid(self.linear(x))
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
model = BinaryClassifier()
# optimizer 설정
optimizer = optim.SGD(model.parameters(), lr=1)
nb_epochs = 100
for epoch in range(nb_epochs + 1):
# H(x) 계산
hypothesis = model(x_train)
# cost 계산
cost = F.binary_cross_entropy(hypothesis, y_train)
# cost로 H(x) 개선
optimizer.zero_grad()
cost.backward()
optimizer.step()
# 20번마다 로그 출력
if epoch % 10 == 0:
prediction = hypothesis >= torch.FloatTensor([0.5])
correct_prediction = prediction.float() == y_train
accuracy = correct_prediction.sum().item() / len(correct_prediction)
print('Epoch {:4d}/{} Cost: {:.6f} Accuracy {:2.2f}%'.format(
epoch, nb_epochs, cost.item(), accuracy * 100,
))
'''output
Epoch 0/100 Cost: 0.704829 Accuracy 45.72%
Epoch 10/100 Cost: 0.572391 Accuracy 67.59%
Epoch 20/100 Cost: 0.539563 Accuracy 73.25%
Epoch 30/100 Cost: 0.520042 Accuracy 75.89%
Epoch 40/100 Cost: 0.507561 Accuracy 76.15%
Epoch 50/100 Cost: 0.499125 Accuracy 76.42%
Epoch 60/100 Cost: 0.493177 Accuracy 77.21%
Epoch 70/100 Cost: 0.488846 Accuracy 76.81%
Epoch 80/100 Cost: 0.485612 Accuracy 76.28%
Epoch 90/100 Cost: 0.483146 Accuracy 76.55%
Epoch 100/100 Cost: 0.481234 Accuracy 76.81%
'''
학습이 정상적으로 된 것을 확인할 수 있다. 이때 accuracy는 correct_prediction에 맞았는지 틀렸는지를 저장해 평균을 내어 계산한다.