모두를 위한 딥러닝 2 - Lab3: Minimizing Cost

모두를 위한 딥러닝 Lab 3: Minimizing Cost 강의를 본 후 공부를 목적으로 작성한 게시물입니다.

---

Theoretical Overview

이번에는 Grdient descent에 대해 조금 더 집중적으로 알아보기 위해 Hypothesis를 조금 더 단순하게 $ H(x) = Wx $로 바꾸어 살펴보자.

cost는 똑같이 MSE(Mean Square Error)를 사용하고 데이터도 이전과 같은 공부 시간 - 성적 데이터를 사용한다. (Lab2 포스팅 참조)

\[ MSE = cost(W) = \frac{1}{m} \sum^m_{i=1} \left( H(x^{(i)}) - y^{(i)} \right)^2 \]

---

Import

import matplotlib.pyplot as plt
import numpy as np
import torch
import torch.nn as nn
import torch.nn.functional as F
import torch.optim as optim

---

Cost by W

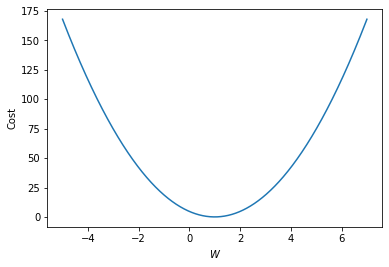
W의 변화에 따른 cost 그래프를 그려보면 다음과 같은 2차 곡선이 그려진다. 그러므로 cost가 가장 작은 점은 기울기(미분값)가 0인 극소점이다.

W_l = np.linspace(-5, 7, 1000)
cost_l = []
for W in W_l:
    hypothesis = W * x_train
    cost = torch.mean((hypothesis - y_train) ** 2)

    cost_l.append(cost.item())

plt.plot(W_l, cost_l)
plt.xlabel('$W$')
plt.ylabel('Cost')
plt.show()

---

Gradient Descent by Hand

cost가 가장 작은 점을 찾는 것이 우리의 목표인데, 이것을 cost의 미분값을 이용하는 방식으로 달성하려고 한다.

cost는 다음과 같으므로

\[ MSE = cost(W) = \frac{1}{m} \sum^m_{i=1} \left( H(x^{(i)}) - y^{(i)} \right)^2 \]

$W$에 대해 미분하면 아래와 같은 결과를 얻을 수 있다.

\[ \nabla W = \frac{\partial cost}{\partial W} = \frac{2}{m} \sum^m_{i=1} \left( Wx^{(i)} - y^{(i)} \right)x^{(i)} \]

이렇게 구한 gradient는 다음 식과 같이 학습에 적용하게 된다.

\[ W := W - \alpha \nabla W \,\,\left(\alpha = learning\,\,rate\right)\]

이런 형태로 학습을 하는 이유를 한번 알아보자.

아래의 두 gif는 각각 극소점의 좌우에서 극소점에 접근할 때 접선의 변화를 나타낸 것이다.



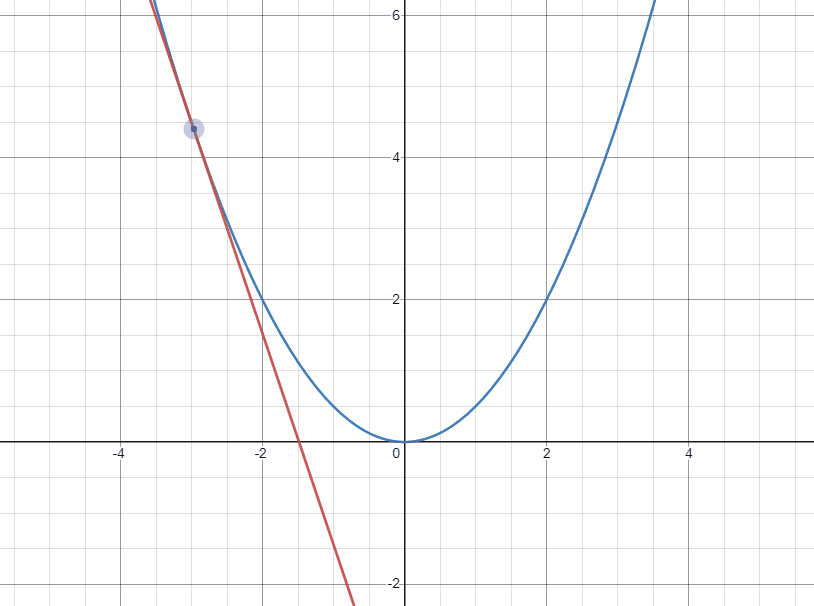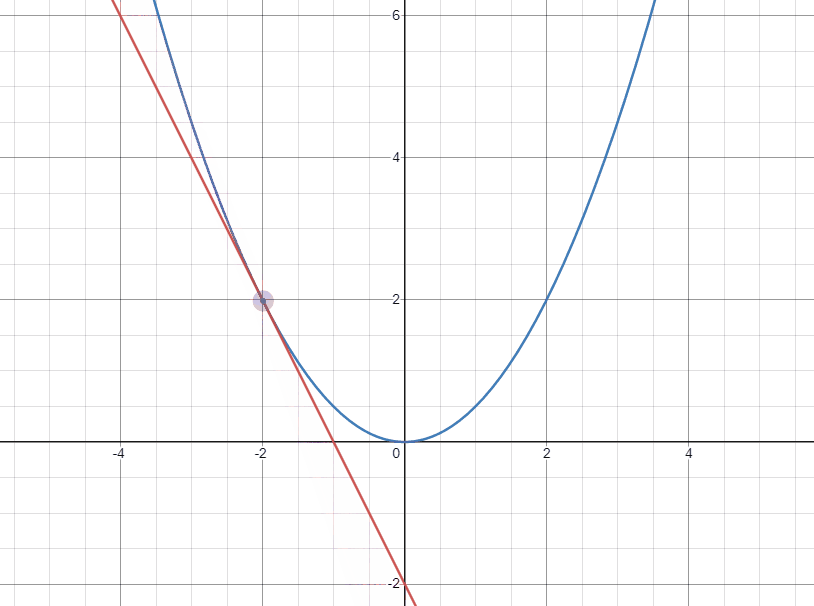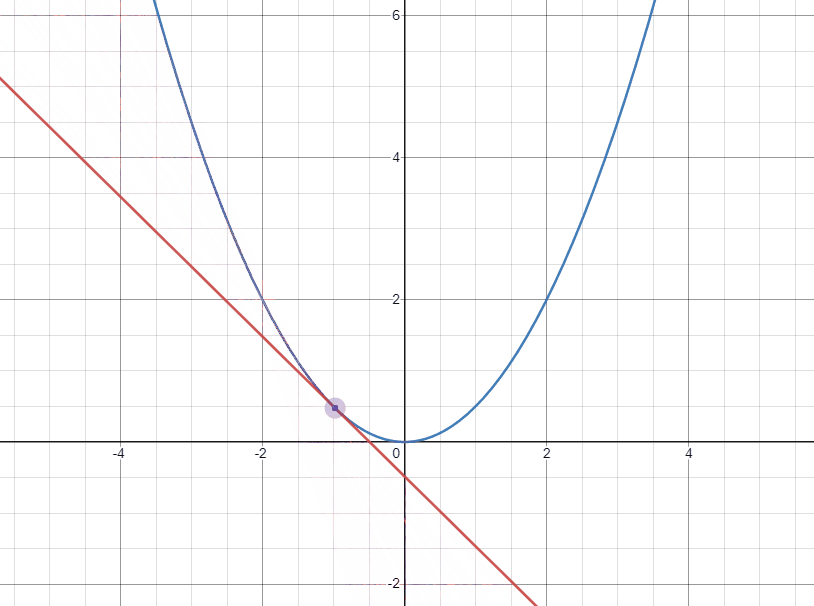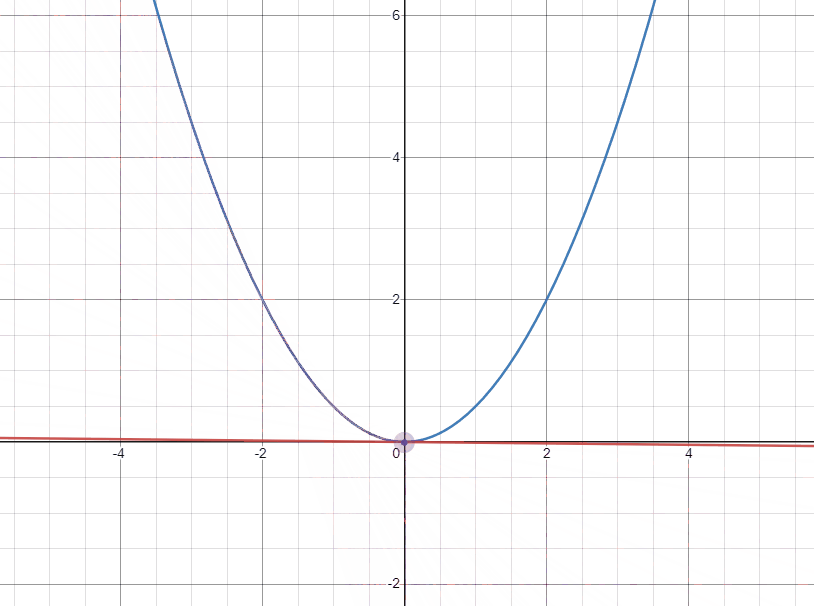
먼저 왼쪽에서 접근하는 경우 기울기(gradient)가 음수이고 극소점으로 도달하기 위해서는 $W$가 커져야 한다. 그러므로 음수인 기울기를 빼주어 극소점에 가깝게 도달할 수 있다.



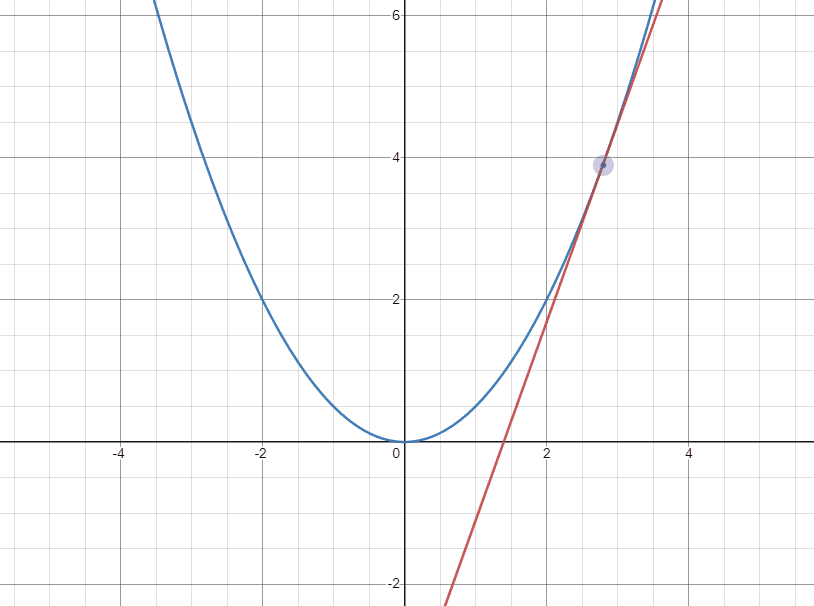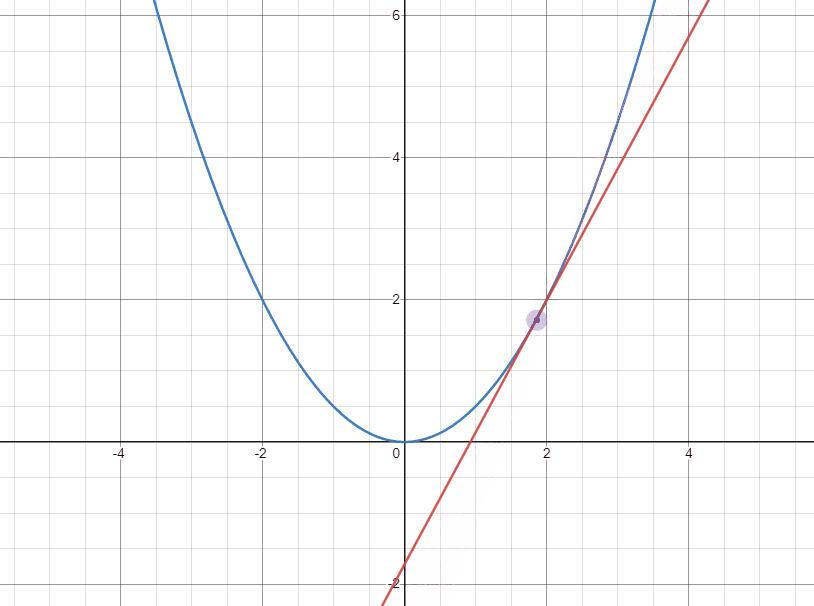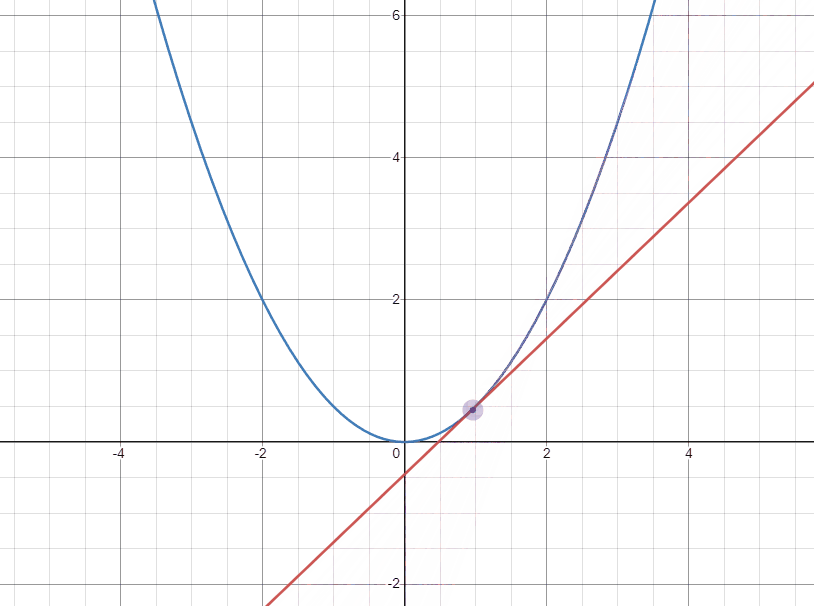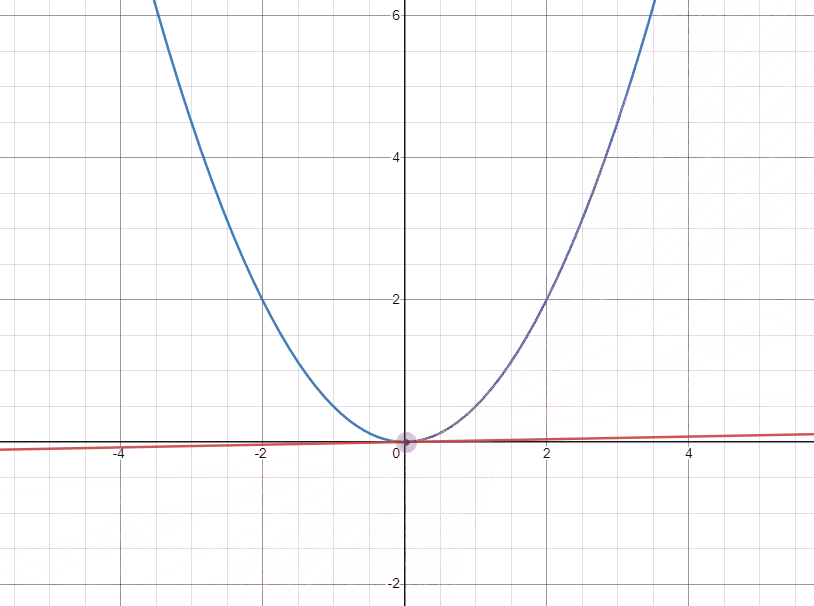
다음으로 오른쪽에서 접근하는 경우 기울기가 양수이고 극소점으로 도달하기 위해서는 $W$가 작아져야 한다. 이 때는 양수인 기울기를 빼주어 극소점에 가깝게 도달할 수 있다.

결국 이 둘다 빼야하므로 모두 만족하는 식이 $ W := W - \alpha \nabla W $, 기울기의 뺄셈으로 주어지는 것이다. 이 때 $learning\,\,rate$인 $\alpha$는 말 그대로 학습률(한 번에 학습을 얼마나 할 것인가)을 나타내는 것이므로 상황에 맞게 최적화 하여 사용한다.

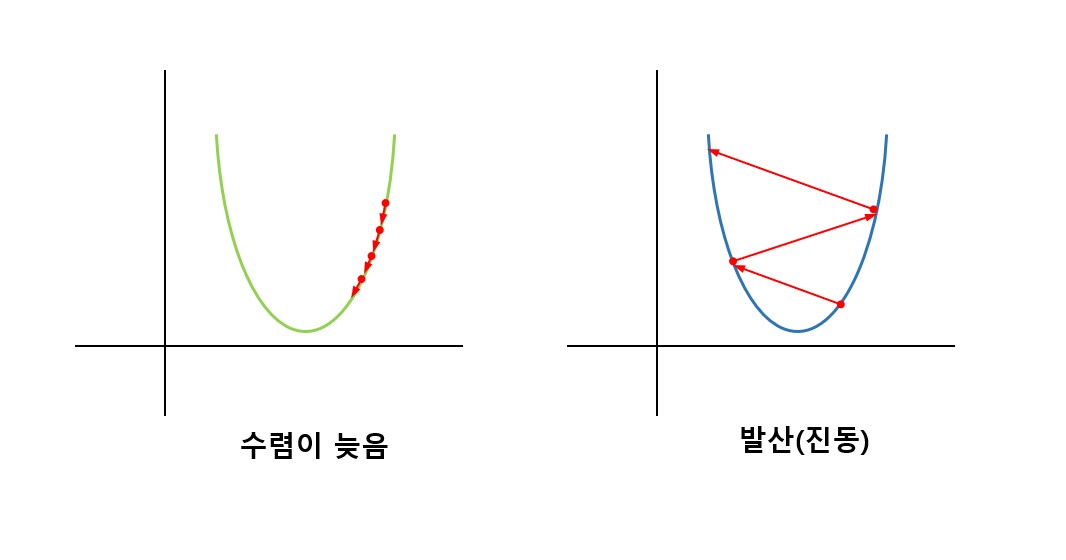
다만, 학습률이 너무 작으면 수렴이 늦어지고, 너무 크면 진동하면 발산해 버리기 때문에 적절한 범위의 값을 사용해야 한다.

이어서 앞선 식들을 코드로 표현하면 다음과 같다.

\[ \nabla W = \frac{\partial cost}{\partial W} = \frac{2}{m} \sum^m_{i=1} \left( Wx^{(i)} - y^{(i)} \right)x^{(i)} \]

gradient = torch.sum((W * x_train - y_train) * x_train)
print(gradient)

''' output
tensor(-14.)
'''

\[ W := W - \alpha \nabla W \,\,\left(\alpha = learning\,\,rate\right)\]

lr = 0.1
W -= lr * gradient
print(W)

''' output
tensor(1.4000)
'''

---

Training

앞서 구현했던 것들을 활용하여 실제로 학습하는 코드를 작성해 보면 다음과 같다.

# 데이터
x_train = torch.FloatTensor([[1], [2], [3]])
y_train = torch.FloatTensor([[1], [2], [3]])
# 모델 초기화
W = torch.zeros(1)
# learning rate 설정
lr = 0.1

nb_epochs = 10
for epoch in range(nb_epochs + 1):

    # H(x) 계산
    hypothesis = x_train * W

    # cost gradient 계산
    cost = torch.mean((hypothesis - y_train) ** 2)
    gradient = torch.sum((W * x_train - y_train) * x_train)

    print('Epoch {:4d}/{} W: {:.3f}, Cost: {:.6f}'.format(
        epoch, nb_epochs, W.item(), cost.item()
    ))

    # gradient로 H(x) 개선
    W -= lr * gradient

''' output
Epoch    0/10 W: 0.000, Cost: 4.666667
Epoch    1/10 W: 1.400, Cost: 0.746666
Epoch    2/10 W: 0.840, Cost: 0.119467
Epoch    3/10 W: 1.064, Cost: 0.019115
Epoch    4/10 W: 0.974, Cost: 0.003058
Epoch    5/10 W: 1.010, Cost: 0.000489
Epoch    6/10 W: 0.996, Cost: 0.000078
Epoch    7/10 W: 1.002, Cost: 0.000013
Epoch    8/10 W: 0.999, Cost: 0.000002
Epoch    9/10 W: 1.000, Cost: 0.000000
Epoch   10/10 W: 1.000, Cost: 0.000000
'''

Hypothesis output 계산 -> cost와 gradient 계산 -> gradient로 hypothesis(weight) 개선

위와 같은 순서로 총 10 epoch 학습하는 코드이다. 학습을 한번 할 때마다 cost가 줄어들고, 우리가 생각한 이상적인 $W$인 1에 점점 가까워지는 것을 확인할 수 있다.

---

Training with optim

Training에서 했던 것처럼 우리가 gradient를 계산하는 코드를 직접 작성하여 사용할 수도 있지만 PyTorch에서 제공하는 optim을 이용하여 간단하게 구현할 수도 있다.

# 데이터
x_train = torch.FloatTensor([[1], [2], [3]])
y_train = torch.FloatTensor([[1], [2], [3]])
# 모델 초기화
W = torch.zeros(1, requires_grad=True)
# optimizer 설정
optimizer = optim.SGD([W], lr=0.15)

nb_epochs = 10
for epoch in range(nb_epochs + 1):

    # H(x) 계산
    hypothesis = x_train * W

    # cost 계산
    cost = torch.mean((hypothesis - y_train) ** 2)

    print('Epoch {:4d}/{} W: {:.3f} Cost: {:.6f}'.format(
        epoch, nb_epochs, W.item(), cost.item()
    ))

    # cost로 H(x) 개선
    optimizer.zero_grad()
    cost.backward()
    optimizer.step()

''' output
Epoch    0/10 W: 0.000 Cost: 4.666667
Epoch    1/10 W: 1.400 Cost: 0.746667
Epoch    2/10 W: 0.840 Cost: 0.119467
Epoch    3/10 W: 1.064 Cost: 0.019115
Epoch    4/10 W: 0.974 Cost: 0.003058
Epoch    5/10 W: 1.010 Cost: 0.000489
Epoch    6/10 W: 0.996 Cost: 0.000078
Epoch    7/10 W: 1.002 Cost: 0.000013
Epoch    8/10 W: 0.999 Cost: 0.000002
Epoch    9/10 W: 1.000 Cost: 0.000000
Epoch   10/10 W: 1.000 Cost: 0.000000
'''

optim.SGD가 우리가 만들어서 구현했던 gradient에 대한 처리를 해주고 있는 것을 볼 수 있다.

optimizer.zero_grad() # gradient 초기화
cost.backward()       # gradient 계산
optimizer.step()      # 계산된 gradient를 따라 W, b를 개선

저번 강의에서도 등장했던 위 3개의 묶음 코드를 통해 gradient에 대한 계산과 그에 따른 학습이 이루어지고 있다.

이 때도 마찬가지로 $W$와 cost를 보면 잘 학습이 되는 것을 볼 수 있다.