모두를 위한 딥러닝 2 - Lab2: Linear regression
모두를 위한 딥러닝 Lab 2: Linear regression 강의를 본 후 공부를 목적으로 작성한 게시물입니다.
Theoretical Overview
Hypothesis (가설)
선형 회귀에서 사용하는 1차 방정식을 말한다. weight와 bias를 계속 바꿔가면거 마지막 학습이 끝난 뒤의 최종값을 사용하여 데이터를 예측한다. 수식은 다음과 같다.
\[ H(x) = Wx + b \]
최종 결과로 나온 가설을 model이라 하고 ‘학습되었다’고 한다.
Cost
model의 예측 값이 실제 값과 얼마나 다른 지를 알려준다. (작을수록 좋은 모델이다.)
여기서는 아래와 같은 MSE(Mean Square Error)를 사용한다.
\[ MSE = cost(W, b) = \frac{1}{m} \sum^m_{i=1} \left( H(x^{(i)}) - y^{(i)} \right)^2 \]
Import
import torch
import torch.nn as nn
import torch.nn.functional as F
import torch.optim as optimData
데이터는 다음과 같이 간단한 공부 시간 - 성적 데이터 셋을 사용한다.
| 공부 시간 | 성적 |
|---|---|
| 1 | 1 |
| 2 | 2 |
| 3 | 3 |
x_train = torch.FloatTensor([[1], [2], [3]])
y_train = torch.FloatTensor([[1], [2], [3]])공부 시간이 각각 1시간에서 3시간일 때 그 점수도 1시간에서 3시간인 데이터 셋이다.
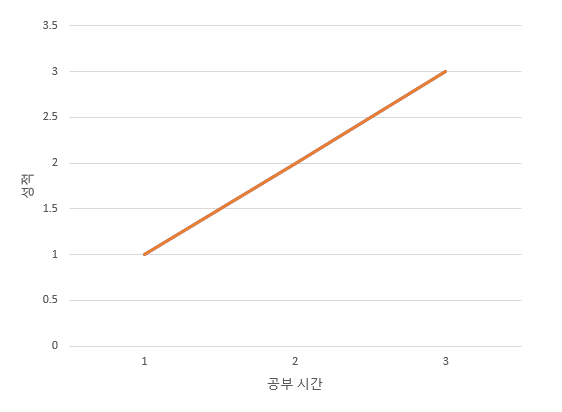
이런 데이터셋일 때 가장 이상적인 회귀선을 한번 생각해 보자.
위와 같은 $ y = x $ 꼴의 직선이 가장 이상적일 것이다. 그러므로 이후 학습을 진행할 때 weight=1, bias=0에 가까워 지는지 확인하면 학습이 잘 이루어지고 있는지 알 수 있을 것이다.
Weight Initialization
W = torch.zeros(1, requires_grad=True)
print(W)
b = torch.zeros(1, requires_grad=True)
print(b)
''' output
tensor([0.], requires_grad=True)
tensor([0.], requires_grad=True)
'''학습할 weight와 bias를 모두 0으로 초기화 해 준다.
Hypothesis
\[ H(x) = Wx + b \]
앞서 보았던 Hypothesis 식에 따라 초기화해 준다.
hypothesis = x_train * W + b
print(hypothesis)
''' output
tensor([[0.],
[0.],
[0.]], grad_fn=<AddBackward0>)
'''초기 weight와 bias는 모두 0이므로 모든 값이 0으로 나온 것을 볼 수 있다.
Cost
\[ MSE = cost(W, b) = \frac{1}{m} \sum^m_{i=1} \left( H(x^{(i)}) - y^{(i)} \right)^2 \]
Cost도 마찬가지로 앞서 나온 식에 맞춰 정의해 준다.
cost = torch.mean((hypothesis - y_train) ** 2)
print(cost)
''' output
tensor(4.6667, grad_fn=<MeanBackward1>)
'''Gradient Descent
optim을 통해 SGD optimer를 불러 사용한다. Gradient Descent에 대한 내용은 다음 포스팅에서 더 자세하게 살펴 볼 예정이다.
optimizer = optim.SGD([W, b], lr=0.01)그리고 PyTorch에서 학습을 할 때 항상 묶어 쓰는 코드들이 있다.
optimizer.zero_grad() # gradient 초기화
cost.backward() # gradient 계산
optimizer.step() # 계산된 gradient를 따라 W, b를 개선
print(W)
print(b)
''' output
tensor([0.0933], requires_grad=True)
tensor([0.0400], requires_grad=True)
'''위 3개의 코드는 gradient를 초기화 하고, cost에 따라 계산하고, 그 결과에 따라 weight와 bias를 개선하는 과정이다. 학습할 때 필요한 부분이므로 외워두어야 한다.
gradient를 계산할 때 각 시행마다 optimizer.zero_grad()로 gradient를 초기화하는 이유는 cost.backward()가 계산을 하고 기존 gradient를 대체하는 것이 아니라 더하기 때문이라고 한다.(DNN에서의 backpropagation을 할 때 유용하기 때문) 그래서 optimizer.zero_grad()를 통해 초기화해 주지 않으면 전 시행의 gradient와 현재의 것이 누적되어 잘못된 방향으로 학습되게 된다.
위 코드를 한 번 실행한 것이 한 번 학습한 것과 같다. 그 결과에 따라 weight와 bias의 개선이 이루어진 것을 볼 수 있다.
개선된 weight와 bias로 다시 예측을 해 보면, 다음과 같은 값을 얻을 수 있다.
hypothesis = x_train * W + b
print(hypothesis)
cost = torch.mean((hypothesis - y_train) ** 2)
print(cost)
''' output
tensor([[0.1333],
[0.2267],
[0.3200]], grad_fn=<AddBackward0>)
tensor(3.6927, grad_fn=<MeanBackward0>)
'''기존에 0이었던 값들이 실제 값에 가깝게 변했고, cost도 줄어든 것을 확인할 수 있다.
Training with Full Code
# 데이터
x_train = torch.FloatTensor([[1], [2], [3]])
y_train = torch.FloatTensor([[1], [2], [3]])
# 모델 초기화
W = torch.zeros(1, requires_grad=True)
b = torch.zeros(1, requires_grad=True)
# optimizer 설정
optimizer = optim.SGD([W, b], lr=0.01)
nb_epochs = 1000
for epoch in range(nb_epochs + 1):
# H(x) 계산
hypothesis = x_train * W + b
# cost 계산
cost = torch.mean((hypothesis - y_train) ** 2)
# cost로 H(x) 개선
optimizer.zero_grad()
cost.backward()
optimizer.step()
# 100번마다 로그 출력
if epoch % 100 == 0:
print('Epoch {:4d}/{} W: {:.3f}, b: {:.3f} Cost: {:.6f}'.format(
epoch, nb_epochs, W.item(), b.item(), cost.item()
))
''' output
Epoch 0/1000 W: 0.093, b: 0.040 Cost: 4.666667
Epoch 100/1000 W: 0.873, b: 0.289 Cost: 0.012043
Epoch 200/1000 W: 0.900, b: 0.227 Cost: 0.007442
Epoch 300/1000 W: 0.921, b: 0.179 Cost: 0.004598
Epoch 400/1000 W: 0.938, b: 0.140 Cost: 0.002842
Epoch 500/1000 W: 0.951, b: 0.110 Cost: 0.001756
Epoch 600/1000 W: 0.962, b: 0.087 Cost: 0.001085
Epoch 700/1000 W: 0.970, b: 0.068 Cost: 0.000670
Epoch 800/1000 W: 0.976, b: 0.054 Cost: 0.000414
Epoch 900/1000 W: 0.981, b: 0.042 Cost: 0.000256
Epoch 1000/1000 W: 0.985, b: 0.033 Cost: 0.000158
'''1000 Epoch 학습하는 전체 코드이다. 로그에서 알 수 있듯이 cost는 점점 줄어들고 weight와 bias도 우리가 예상했던 회귀선의 것과 비슷해졌다.
x_train * W + b
''' output
tensor([[1.0186],
[2.0040],
[2.9894]], grad_fn=<AddBackward0>)
'''실제로 학습된 모델로 예측을 해 보면 실제 값과 아주 비슷하게 나온 것을 확인할 수 있다.