모두를 위한 딥러닝 2 - Lab11-4: Timeseries
모두를 위한 딥러닝 Lab11-4: Timeseries 강의를 본 후 공부를 목적으로 작성한 게시물입니다.
Timeseries
timeseries(시게열) data는 일정 시간 간격으로 배치된 data를 말한다. 매장의 시간별 매출, 요일별 주식 시가/종가 등이 여기에 속할 수 있다. 이들도 순서가 데이터에 포함된 경우이므로 RNN을 이용하여 과거의 데이터를 가지고 예측을 하는 것이 좋은 방법일 수 있다. (순서를 포함한 데이터라고 RNN이 만능이라는 것은 아니다.)
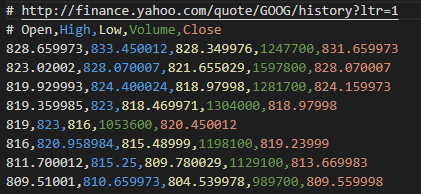
이번 실습에서는 요일별 주식 정보들을 이용하여 학습을 진행하였다.
위와 같이 일별 시작가, 고가, 저가, 거래량, 종가가 포함된 데이터이다.
이 데이터를 그냥 학습시킬수도 있지만 각 데이터들의 scale을 맞추고 하는 것이 더 좋다. 거래량을 제외한 가격 정보들은 800 정도의 값에 있지만 거래량은 100만 단위이다. 만약 이대로 바로 학습한다면 거래량에 치우쳐서 학습을 하거나 scale을 맞추기 위한 학습을 model이 추가적으로 해야 하므로 필요없는 부담이 발생할 수 있다. 그래서 뒤에 나올 코드에서는 scaling을 하고 학습을 진행할 것이다.
with Code
Imports
1
2
3
4
5
6
7
8
9
10
11
12
13
14
import torch
import torch.optim as optim
import numpy as np
import matplotlib.pyplot as plt
torch.manual_seed(0)
# hyper parameters
seq_length = 7
data_dim = 5
hidden_dim = 10
output_dim = 1
learning_rate = 0.01
iterations = 500
Data
데이터를 불러오고 70%의 데이터를 train data로 만들어준다.
1
2
3
4
5
6
7
8
# load data
xy = np.loadtxt("data-02-stock_daily.csv", delimiter=",")
xy = xy[::-1] # reverse order
# split train-test set
train_size = int(len(xy) * 0.7)
train_set = xy[0:train_size]
test_set = xy[train_size - seq_length:]
앞서 언급한대로 scaling을 하고 학습하기 좋은 형태로 data를 가공해야 한다.
1
2
3
4
5
6
7
def minmax_scaler(data):
numerator = data - np.min(data, 0)
denominator = np.max(data, 0) - np.min(data, 0)
return numerator / (denominator + 1e-7)
train_set = minmax_scaler(train_set)
test_set = minmax_scaler(test_set)
이번 에제에서는 min-max scaling을 적용할 것이다. min-max scaling은 아래 식을 통해 진행되는 scaling으로 최소, 최대값을 사용하여 0과 1사이의 값으로 바꾸어 준다.
\[x_{scaled}=\frac{x-x_{min}}{x_{max}-x_{min}}\]
이번에도 데이터의 길이가 길기 때문에 RNN model에 넣어줄 만큼 잘라서 데이터를 만들어준다.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
def build_dataset(time_series, seq_length):
dataX = []
dataY = []
for i in range(0, len(time_series) - seq_length):
_x = time_series[i:i + seq_length, :]
_y = time_series[i + seq_length, [-1]] # Next close price
print(_x, "->", _y)
dataX.append(_x)
dataY.append(_y)
return np.array(dataX), np.array(dataY)
trainX, trainY = build_dataset(train_set, seq_length)
testX, testY = build_dataset(test_set, seq_length)
'''output
[[2.53065030e-01 2.45070970e-01 2.33983036e-01 4.66075110e-04
2.32039560e-01]
[2.29604366e-01 2.39728936e-01 2.54567513e-01 2.98467330e-03
2.37426028e-01]
[2.49235510e-01 2.41668371e-01 2.48338489e-01 2.59926504e-04
2.26793794e-01]
[2.21013495e-01 2.46602231e-01 2.54710584e-01 0.00000000e+00
2.62668239e-01]
[3.63433786e-01 3.70389871e-01 2.67168847e-01 1.24764722e-02
2.62105010e-01]
[2.59447633e-01 3.10673724e-01 2.74113889e-01 4.56323384e-01
2.71751265e-01]
[2.76008150e-01 2.78314566e-01 1.98470380e-01 5.70171193e-01
1.78104644e-01]] -> [0.16053716]
...
[0.88723699 0.88829938 0.92518158 0.08714288 0.90908564]
[0.88939504 0.88829938 0.94014512 0.13380794 0.90030461]
[0.89281215 0.89655181 0.94323484 0.12965206 0.93124657]
[0.91133638 0.91818448 0.95944078 0.1885611 0.95460261]] -> [0.97604677]
'''
7일간의 주식 데이터(x)들을 통해 그 다음날의 종가(y)를 예측하도록 데이터를 만든다. window의 크기를 7로 해서 잘랐다고 생각하면 될것 같다.
Model
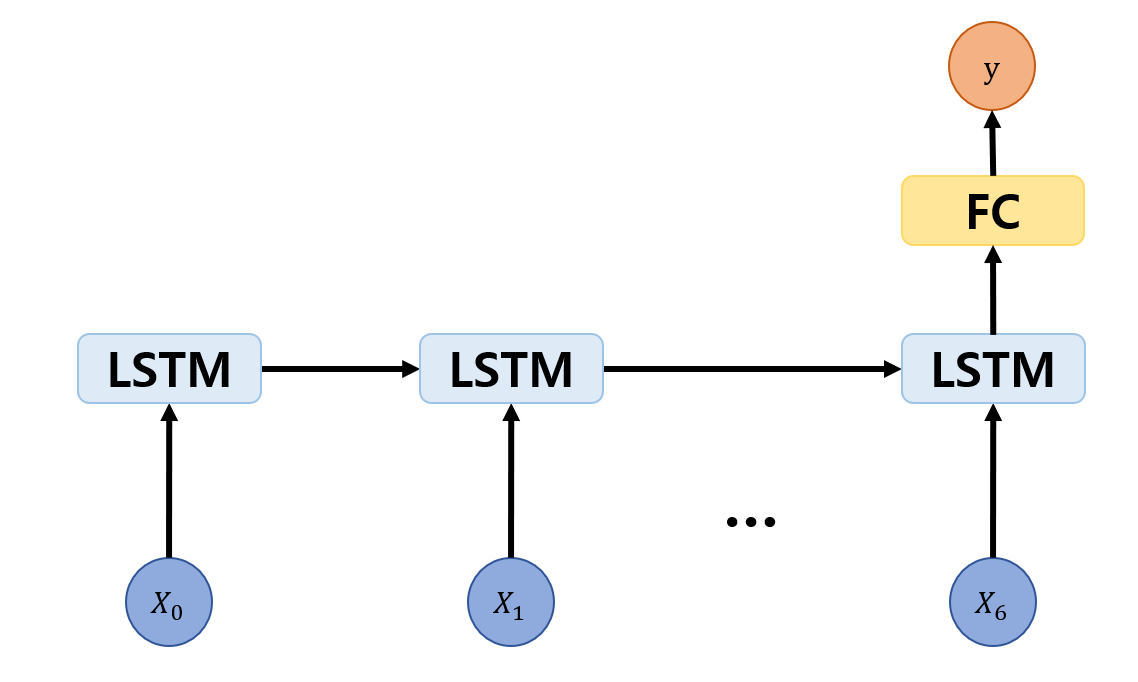
이번에는 RNN의 한 종류인 LSTM을 사용하며 마지막에 fully connected layer를 연결하여 출력을 낸다.
이런 식으로 마지막에 fc 층을 추가하는 이유가 몇가지 있다.
먼저, data를 전달하는 부분과 label을 최종적으로 맞추는 부분을 분리하여 network에 가해지는 부담을 분산할 수 있다. 그리고 RNN 층을 바로 출력에 연결할 경우 과거의 정보를 전달하는 hidden state도 최종 출력의 차원과 맞춰주어야 한다. 이번 경우를 보면 최종적으로 1차원의 출력을 내어야 하는데 이는 정보를 전달하는 hidden state도 차원이 1이어야 한다는 뜻이다. 이런 상황에서는 model이 학습 뿐만 아니라 전보 전달을 위한 압축도 해야하는 부담을 가지게 되어 학습에 악영향을 끼칠 수 있다. 그래서 일반적으로 hidden state의 차원은 충분히 보장해주고 마지막에 fc layer를 연결하여 출력을 완성하는 방식을 사용한다.
1
2
3
4
5
6
7
8
9
10
11
12
13
class Net(torch.nn.Module):
def __init__(self, input_dim, hidden_dim, output_dim, layers):
super(Net, self).__init__()
self.rnn = torch.nn.LSTM(input_dim, hidden_dim, num_layers=layers, batch_first=True)
self.fc = torch.nn.Linear(hidden_dim, output_dim, bias=True)
def forward(self, x):
x, _status = self.rnn(x)
x = self.fc(x[:, -1])
return x
net = Net(data_dim, hidden_dim, output_dim, 1)
Train
loss와 optimizer를 정의하고 학습한다.
1
2
3
4
5
6
7
8
9
10
11
criterion = torch.nn.MSELoss()
optimizer = optim.Adam(net.parameters(), lr=learning_rate)
for i in range(iterations):
optimizer.zero_grad()
outputs = net(trainX_tensor)
loss = criterion(outputs, trainY_tensor)
loss.backward()
optimizer.step()
print(i, loss.item())
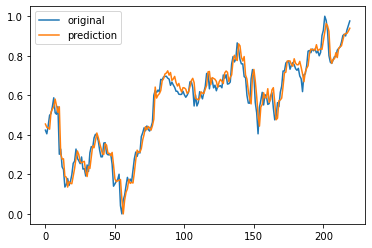
예측한 것들을 크래프로 그려보면 다음과 같다
1
2
3
4
plt.plot(testY)
plt.plot(net(testX_tensor).data.numpy())
plt.legend(['original', 'prediction'])
plt.show()
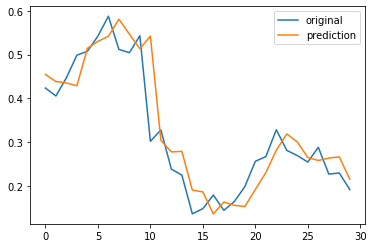
예측이 아주 잘 된것 같아 보이지만 실제로는 아니다.
위 그림은 그래프 중 일부를 가져온 것인데, 잘 보면 예측이 오른쪽으로 한 칸씩 밀린 것처럼 보인다. 이는 노이즈가 심한 금융 시계열 데이터에서 lstm model의 고질적인 문제로 직전 값을 예측 값으로 출력하는 경우가 잦다고 한다. (이전의 값을 예측 값으로 내는 것이 가장 이득이라고 판단했기 때문) 실제로 사용할 때에는 이런 경우에 정말로 예측을 잘 한 것인지 아니면 위와 같이 밀려서 잘 되어 보이는 건지 확인해 볼 필요가 있을 것 같다.