[SWEA]벌꿀 채취 - 2115 (모의 역량 테스트)
| 시간 제한 | 메모리 제한 |
|---|---|
| 6 초 | 힙 정적 메모리: 256 MB / 스택 메모리 1MB |
문제
N*N 개의 벌통이 정사각형 모양으로 배치되어 있다.
각 칸의 숫자는 각각의 벌통에 있는 꿀의 양을 나타내며, 꿀의 양은 서로 다를 수 있다.
각 벌통에 있는 꿀의 양이 주어졌을 때, 다음과 같은 과정으로 벌꿀을 채취하여 최대한 많은 수익을 얻으려고 한다.
두 명의 일꾼이 있다. 꿀을 채취할 수 있는 벌통의 수 M이 주어질 때, 각각의 일꾼은 가로로 연속되도록 M개의 벌통을 선택하고, 선택한 벌통에서 꿀을 채취할 수 있다. 단, 두 명의 일꾼이 선택한 벌통은 서로 겹치면 안 된다.
두 명의 일꾼은 선택한 벌통에서 꿀을 채취하여 용기에 담아야 한다. 단, 서로 다른 벌통에서 채취한 꿀이 섞이게 되면 상품가치가 떨이지게 되므로, 하나의 벌통에서 채취한 꿀은 하나의 용기에 담아야 한다. 하나의 벌통에서 꿀을 채취할 때, 일부분만 채취할 수 없고 벌통에 있는 모든 꿀을 한번에 채취해야 한다. 두 일꾼이 채취할 수 있는 꿀의 최대 양은 C 이다.
채취한 꿀은 시장에서 팔리게 된다. 이때 하나의 용기에 있는 꿀의 양이 많을수록 상품가치가 높아, 각 용기에 있는 꿀의 양의 제곱만큼의 수익이 생긴다.
벌통들의 크기 N과 벌통에 있는 꿀의 양에 대한 정보, 선택할 수 있는 벌통의 개수 M, 꿀을 채취할 수 있는 최대 양 C가 주어진다.
이때 두 일꾼이 꿀을 채취하여 얻을 수 있는 수익의 합이 최대가 되는 경우를 찾고, 그 때의 최대 수익을 출력하는 프로그램을 작성하라.
제약 사항
시간제한 : 최대 50개 테스트 케이스를 모두 통과하는데, C/C++/Java 모두 3초.
벌통들의 크기 N은 3 이상 10 이하의 정수이다. (3 ≤ N ≤ 10)
선택할 수 있는 벌통의 개수 M은 1 이상 5 이하의 정수이다. (1 ≤ M ≤ 5)
선택할 수 있는 벌통의 개수 M은 반드시 N 이하로만 주어진다.
꿀을 채취할 수 있는 최대 양 C는 10 이상 30 이하의 정수이다. (10 ≤ C ≤ 30)
하나의 벌통에서 채취할 수 있는 꿀의 양은 1 이상 9 이하의 정수이다.
하나의 벌통에서 일부분의 꿀만 채취할 수 없고, 벌통에 있는 모든 꿀을 한번에 채취해야 한다.
입력
입력의 맨 첫 줄에는 총 테스트 케이스의 개수 T가 주어지고, 그 다음 줄부터 T개의 테스트 케이스가 주어진다.
각 테스트 케이스의 첫 번째 줄에는 벌통들의 크기 N, 선택할 수 있는 벌통의 개수 M, 꿀을 채취할 수 있는 최대 양 C가 차례로 주어진다.
그 다음 줄부터 N*N 개의 벌통에서 채취할 수 있는 꿀의 양에 대한 정보가 주어진다.
출력
테스트 케이스의 개수만큼 T줄에 T개의 테스트 케이스 각각에 대한 답을 출력한다.
각 줄은 “#x”로 시작하고 공백을 하나 둔 다음 정답을 출력한다. (x는 1부터 시작하는 테스트 케이스의 번호이다)
출력해야 할 정답은 두 일꾼이 꿀을 채취하여 얻을 수 있는 최대 수익이다.
풀이
일종의 완전탐색을 기반으로 가지치기를 해야 한다고 생각했다.
두 사람이 벌통을 선택할 수 있는 방법을 모두 탐색하는 것을 기반으로 진행한다. 탐색하면서 고른 벌통에 대해 부분집합을 만들어 제곱의 합이 최대가 되는 경우를 찾는다. 최대가 되는 제곱의 합이 바로 고른 벌통들에서 나올 수 있는 최대 수익이 된다.
이 때 꿀의 양이 c를 넘는 경우는 더 이상 부분 집합을 만들 필요가 없기 때문에 연산하지 않는다.
재귀를 통한 풀이
첫 번째로 생각한 방법은 재귀로 부분 집합을 그대로 구해서 계산하는 것이다. 단, 앞서 말한 가지치기를 하기 위해 c를 넘는 경우는 넘어가도록 작성하였다.
코드
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
test_case = int(input())
def make_subset(arr, depth, honey_num = 0, selected = []):
if depth == -1:
subsets.append(selected)
return
for i in range(2):
if i == 0:
make_subset(arr, depth - 1, honey_num, selected)
else:
if honey_num + arr[depth] > c:
continue
make_subset(arr, depth - 1, honey_num + arr[depth], selected + [arr[depth]])
def calcul_max_cost(subsets):
max_cost = 0
for subset in subsets:
cost = 0
for ele in subset:
cost += ele ** 2
max_cost = max(max_cost, cost)
return max_cost
for t in range(test_case):
n, m, c = map(int, input().split())
honey_map = [list(map(int, input().split())) for _ in range(n)]
total_max = 0
for fst_i in range(n):
for fst_j in range(n - m + 1):
subsets = []
make_subset(honey_map[fst_i][fst_j:fst_j + m], m - 1)
fst_max = calcul_max_cost(subsets)
for snd_i in range(n):
start = 0
if snd_i == fst_i:
start = fst_j + m
for snd_j in range(start, n - m + 1):
subsets = []
make_subset(honey_map[snd_i][snd_j:snd_j + m], m - 1)
snd_max = calcul_max_cost(subsets)
total_max = max(total_max, fst_max + snd_max)
print(f"#{t + 1} {total_max}")
DP를 통한 풀이
이 문제를 다시 잘 생각해보면 선택한 꿀통 내에서 꿀통을 고르거나(1) 안고르면서(0) 주어진 c(용량) 내에서 최대의 수익(이득)을 얻는 것이 목적이다. 즉, 이 문제는 0-1 배낭 문제와 유사하므로 DP로도 풀이할 수 있다.
이전에 푼 햄버거 다이어트에서 사용한 DP의 진행 방식과 유사하게 수익을 찾는 풀이이다.
다른 점은 꿀 양의 합이 c를 넘을 경우 DP에 반영하지 않는다는 것과, 제곱의 합이 큰 것을 기준으로 PD에 업데이트한다는 것이다.
부분 집합을 만들어 수익을 계산하는 부분이 DP로 바뀐 것만 제외하면 재귀를 통한 풀이와 완전히 동일하다.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
def max_subset_sum(arr):
dp = [[0, 0] for _ in range(c + 1)]
for num in arr:
for j in range(c, num - 1, -1):
if dp[j - num][0] + num > c:
continue
next_sq_value = dp[j - num][1] + num ** 2
if next_sq_value > dp[j][1]:
dp[j][0] = dp[j - num][0] + num
dp[j][1] = next_sq_value
_, max_sum = max(dp, key=lambda x: x[1])
return max_sum
test_case = int(input())
for t in range(test_case):
n, m, c = map(int, input().split())
honey_map = [list(map(int, input().split())) for _ in range(n)]
total_max = 0
for fst_i in range(n):
for fst_j in range(n - m + 1):
fst_max = max_subset_sum(honey_map[fst_i][fst_j:fst_j + m])
for snd_i in range(n):
start = 0
if snd_i == fst_i:
start = fst_j + m
for snd_j in range(start, n - m + 1):
snd_max = max_subset_sum(honey_map[snd_i][snd_j:snd_j + m])
total_max = max(total_max, fst_max + snd_max)
print(f"#{t + 1} {total_max}")
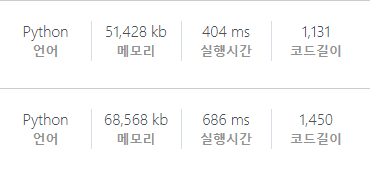
근데 생각보다 실행 시간이 Dynamic하게 줄어들지 않아 살짝 김샜다.