[BOJ]넴모넴모 (Easy) - 14712 (G5)

시간 제한	메모리 제한
1 초	512 MB

문제

네모는 뿌××× 게임에 깊은 감명을 받아, 직사각형 모양의 격자판과 “넴모”라는 수수께끼의 생물을 이용하는 “넴모”모”라는 게임을 만들었다. 이 게임의 규칙은 아주 간단하다. 격자판의 비어 있는 칸을 임의로 골라 “넴모”를 하나 올려놓거나, “넴모”가 올라간 칸 네 개가 2 × 2 사각형을 이루는 부분을 찾아 그 위에 있는 “넴모”들을 모두 없애는 것을 질릴 때까지 반복하면 된다.

하지만 안타깝게도 게임은 정말 재미가 없었고, 네모는 아주 빨리 질려 버리고 말았다. 실망한 네모는 게임을 적당히 플레이하다가, “넴모”를 없애고 싶은데 격자판 위에 없앨 수 있는 “넴모”가 없으면 게임을 그만두기로 했다. 네모가 게임을 그만두었을 때 나올 수 있는 “넴모”의 배치의 가짓수를 구하여라.

입력

첫 번째 줄에 격자판의 행의 개수 N, 열의 개수 M(1 ≤ N, M ≤ 25, 1 ≤ N × M ≤ 25)이 공백으로 구분되어 주어진다.

출력

첫 번째 줄에 주어진 격자판에서 나올 수 있는, “넴모”들이 올라간 칸이 2 × 2 사각형을 이루지 않는 모든 배치의 가짓수를 출력한다.

힌트

2×2 격자판에 2×2 사각형을 이루지 않도록 “넴모”들을 배치하는 방법은 모든 경우(24 = 16) 중 네 칸 모두에 “넴모”가 올라가 있는 경우를 제외한 15가지가 있다.

풀이

DFS 기반의 백트래킹으로 풀었다. 기본적인 DFS 수행은 x축 방향으로 진행하면서 넴모를 놓거나 놓지 않는 방식으로 진행한다.

하지만 굳이 사각형이 완성되는 경우까지 넴모를 놓을 필요는 없으므로 그런 경우는 제외하고 탐색한다.

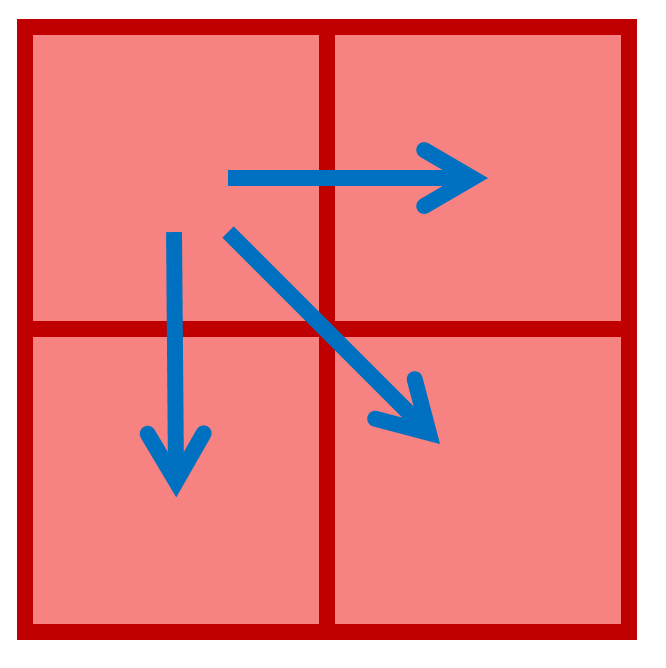
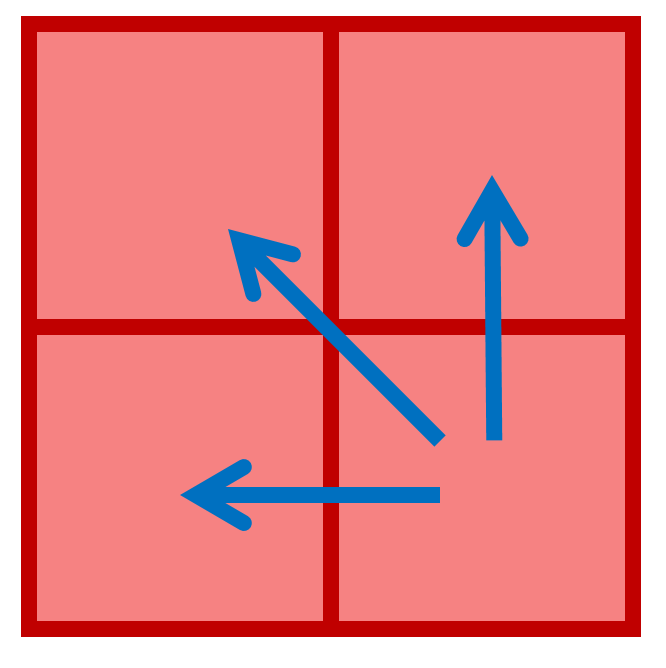
사각형이 완성되는 것은 현재 위치에서 좌상, 좌, 우에 있는 칸을 확인하면 알 수 있다. 만약 다음 그림과 같이 우하, 우, 하에 있는 칸을 확인하면 다음에 놓을 넴모를 미리 알 수 없어 사각형이 완성되는지 확인하기 곤란하다.

그래서 아래와 같이 좌상, 좌, 우를 확인하면서 x축 방향으로 넴모를 놓거나 놓지 않게 탐색을 진행한다.

사방 탐색이 힘든 이유

그냥 우리 많이 하는 것처럼 사방 탐색으로 해버리면 안되냐, 할 수 있다. 하지만 x축 방향으로 차례대로 진행하지 않으면, 위에서 언급한 우하, 우, 하로 사각형을 확인할 때와 같은 문제가 발생한다.

아직 탐색하지 못한(넴모를 놓거나 놓지 못한) 칸에 대해 우리가 사각형인지 판별할 수 없기 때문이다. 그래서 x축 방향(글 쓰는 방향)으로 탐색하면서 이미 탐색이 끝난 칸에 대해서만 사각형을 판별하도록 만들고, 모든 경우에 대해 제대로 넴모를 놓을 수 있게 된다.

코드

def fill_nemo(d=0):
    global cnt
    if N*M == d:
        cnt += 1
        return
    
    y = d // M + 1
    x = d  % M + 1

    # 사각형이 완성 안되는 경우(넴모를 놓을 수 있는 경우)
    if matrix[y-1][x] == 0 or matrix[y-1][x-1] == 0 or matrix[y][x-1] == 0:
        # 다음 위치에 네모 생성
        matrix[y][x] = 1
        fill_nemo(d+1)
        matrix[y][x] = 0

    # 다음 위치에 네모 생성 X
    fill_nemo(d+1)
    

N, M = map(int, input().split())

matrix = [[0]*(M+1) for _ in range(N+1)]

cnt = 0
fill_nemo()

print(cnt)

좌상, 좌, 우를 확인하는데 편리하기 위해 [[0]*(M+1) for _ in range(N+1)]로 한 줄의 padding을 추가했다. 이에 맞춰 x, y도 원래 값보다 +1 하여 사용하였다.