[BOJ] 파일 합치기 - 11066 (G3)
| 시간 제한 | 메모리 제한 |
|---|---|
| 2 초 | 256 MB |
문제
소설가인 김대전은 소설을 여러 장(chapter)으로 나누어 쓰는데, 각 장은 각각 다른 파일에 저장하곤 한다. 소설의 모든 장을 쓰고 나서는 각 장이 쓰여진 파일을 합쳐서 최종적으로 소설의 완성본이 들어있는 한 개의 파일을 만든다. 이 과정에서 두 개의 파일을 합쳐서 하나의 임시파일을 만들고, 이 임시파일이나 원래의 파일을 계속 두 개씩 합쳐서 소설의 여러 장들이 연속이 되도록 파일을 합쳐나가고, 최종적으로는 하나의 파일로 합친다. 두 개의 파일을 합칠 때 필요한 비용(시간 등)이 두 파일 크기의 합이라고 가정할 때, 최종적인 한 개의 파일을 완성하는데 필요한 비용의 총 합을 계산하시오.
예를 들어, C1, C2, C3, C4가 연속적인 네 개의 장을 수록하고 있는 파일이고, 파일 크기가 각각 40, 30, 30, 50 이라고 하자. 이 파일들을 합치는 과정에서, 먼저 C2와 C3를 합쳐서 임시파일 X1을 만든다. 이때 비용 60이 필요하다. 그 다음으로 C1과 X1을 합쳐 임시파일 X2를 만들면 비용 100이 필요하다. 최종적으로 X2와 C4를 합쳐 최종파일을 만들면 비용 150이 필요하다. 따라서, 최종의 한 파일을 만드는데 필요한 비용의 합은 60+100+150=310 이다. 다른 방법으로 파일을 합치면 비용을 줄일 수 있다. 먼저 C1과 C2를 합쳐 임시파일 Y1을 만들고, C3와 C4를 합쳐 임시파일 Y2를 만들고, 최종적으로 Y1과 Y2를 합쳐 최종파일을 만들 수 있다. 이때 필요한 총 비용은 70+80+150=300 이다.
소설의 각 장들이 수록되어 있는 파일의 크기가 주어졌을 때, 이 파일들을 하나의 파일로 합칠 때 필요한 최소비용을 계산하는 프로그램을 작성하시오.
입력
프로그램은 표준 입력에서 입력 데이터를 받는다. 프로그램의 입력은 T개의 테스트 데이터로 이루어져 있는데, T는 입력의 맨 첫 줄에 주어진다.각 테스트 데이터는 두 개의 행으로 주어지는데, 첫 행에는 소설을 구성하는 장의 수를 나타내는 양의 정수 K (3 ≤ K ≤ 500)가 주어진다. 두 번째 행에는 1장부터 K장까지 수록한 파일의 크기를 나타내는 양의 정수 K개가 주어진다. 파일의 크기는 10,000을 초과하지 않는다.
출력
프로그램은 표준 출력에 출력한다. 각 테스트 데이터마다 정확히 한 행에 출력하는데, 모든 장을 합치는데 필요한 최소비용을 출력한다.
풀이
첫 풀이
처음에는 “소설의 여러 장들이 연속이 되도록 파일을 합쳐나가고” 라는 부분을 제대로 읽지 않아 최소값을 계속 뽑으며 파일을 합치려고 했다. 그래서 아래처럼 heapq로 접근하여 풀이를 작성했다.
코드
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
import heapq
T = int(input())
for _ in range(T):
K = int(input())
res = 0
files = list(map(int, input().split()))
heapq.heapify(files)
while len(files) > 1:
a, b = heapq.heappop(files), heapq.heappop(files)
cur = a + b
res += cur
heapq.heappush(files, cur)
print(res)
하지만 파일이 연속이 되도록 합칠 수 없을 뿐더러, 최소값을 뽑으며 파일을 합친다고 해서 전체 비용이 최소가 되는 것이 아니기 때문에 완전히 틀린 접근이었다.
정답 풀이
모든 파일을 합치는 순서를 결정하는 과정은 N 쌍의 괄호를 이용하여 서로 다른 괄호 표현을 구하는 경우의 수인 카탈란 수와 유사하다.
아래와 같이 파일을 합치는 순서를 괄호로 묶어보면, K-1 쌍의 괄호로 서로 다른 괄호 표현을 구하는 것과 같음을 확인할 수 있다. \((((C1 + C2) + C3) + C4)\) \(((C1 + (C2 + C3)) + C4)\) \(((C1 + C2) + (C3 + C4))\) \((C1 + ((C2 + C3) + C4))\) \((C1 + (C2 + (C3 + C4)))\)
카탈란 수는 다음과 같이 계산할 수 있다. \(C_{K-1} = \frac{1}{K}{2K-2\choose K-1}=\frac{(2K-2)!}{(K-1)!(K)!}\)
그러므로 $K=4$일 떄, 가능한 병합 순서는 카탈란 수 $C_3=5$와 같다.
이렇게 생각했을 때 문제에서 주어진 최대 값인 500을 적용한다면 그 최대 경우의 수는 $C_{500}\eqsim6.76*10^{298}\div500$으로 말도 안되는 경우의 수를 보여준다.
그래서 2차원 DP 배열을 다음과 정의하여 해결을 시도하였다.
dp[i][j]는 i 번째에서 j 번째까지의 파일을 합치는 데 필요한 비용의 최소값이다.
이 배열을 다음 과정을 통해 갱신한다.
1
2
3
4
5
6
7
8
...
for i in range(1, K):
for j in range(i, K):
dp[j - i][j] = float('inf')
for k in range(j - i, j):
dp[j - i][j] = min(dp[j - i][j], dp[j - i][k] + dp[k + 1][j])
dp[j - i][j] += sum_list[j + 1] - sum_list[j - i]
...
i는 현재 확인하는 수열의 길이를 뜻한다. i가 2, j가 3이라면 dp에서 갱신하는 부분은 dp[0][1](0번째에서 1번째), dp[1][2](1번째에서 2번째)이다.
각 시행에서 dp[j - i][j]는 min(dp[j - i][j], dp[j - i][k] + dp[k + 1][j])로 갱신되는데, 이는 ‘기존의 값’과 ‘j - i에서 k번째까지의 파일을 합하는데 필요한 최소 비용과 k + 1에서 j번째까지의 파일을 합하는데 필요한 최소 비용을 합한 것’ 중 작은 것을 취한다는 의미이다. 이렇게 하면 기존의 모든 구간에서의 최소 비용을 고려하면서 배열을 갱신할 수 있다.
모든 비교가 끝난 후 해당 구간을 마지막으로 병합하는 데 필요한 비용을 더해준다. 이 비용은 누적합을 이용한다. sum_list에 누적합을 미리 계산해두면 sum_list[j + 1] - sum_list[j - i]만 계산하여 j - i 번째에서 j 번째까지 파일을 병합할 때 발생하는 마지막 비용을 구할 수 있다. 마지막에는 무조건 해당 구간의 모든 수를 더한 만큼 비용이 발생하기 때문이다.
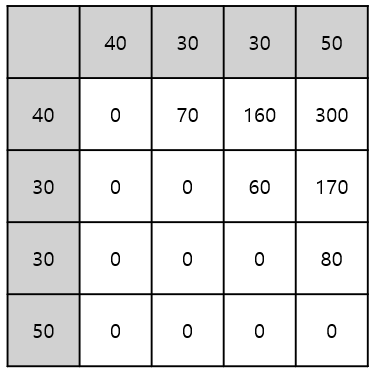
그렇게 계산을 하고 나면 40 30 30 50의 예시에서 dp 배열은 다음과 같이 완성된다.
코드
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
import heapq
T = int(input())
for _ in range(T):
K = int(input())
res = 0
files = list(map(int, input().split()))
dp = [[0] * K for _ in range(K)]
sum_list = [0] * (K + 1)
# 누적합
for i in range(K):
sum_list[i + 1] = sum_list[i] + files[i]
for i in range(1, K):
for j in range(i, K):
dp[j - i][j] = float('inf')
for k in range(j - i, j):
dp[j - i][j] = min(dp[j - i][j], dp[j - i][k] + dp[k + 1][j])
dp[j - i][j] += sum_list[j + 1] - sum_list[j - i]
print(dp[0][K - 1])