[BOJ]Z - 1074 (S1)

시간 제한	메모리 제한
0.5 초	512 MB

tag: divide and conquer, recursion

문제

한수는 크기가 $2^N×2^N$인 2차원 배열을 Z모양으로 탐색하려고 한다. 예를 들어, 2×2배열을 왼쪽 위칸, 오른쪽 위칸, 왼쪽 아래칸, 오른쪽 아래칸 순서대로 방문하면 Z모양이다.

N > 1인 경우, 배열을 크기가 $2^{N-1}×2^{N-1}$로 4등분 한 후에 재귀적으로 순서대로 방문한다.

다음 예는 22 × 2 크기의 배열을 방문한 순서이다.

N이 주어졌을 때, r행 c열을 몇 번째로 방문하는지 출력하는 프로그램을 작성하시오.

다음은 N=3일 때의 예이다.

입력

첫째 줄에 정수 N, r, c가 주어진다.

출력

r행 c열을 몇 번째로 방문했는지 출력한다.

제한

• $1≤N≤15$
• $0≤r,c<2^N$

풀이

수의 크기 제한이 $2^{15}$인 만큼 모두 재귀로 탐색하는 것은 제한 시간을 맞추지 못한다. 보통 1초에 약 $10^8$번의 연산을 한다고 생각하므로 O(N)으로도 해결할 수 없어진다.

그러므로 주어진 x, y가 있는 영역으로 빠르게 다가갈 수 있는 다른 방법을 찾아야 한다. 하나의 큰 Z는 이를 사등분하여 작은 Z를 만들 수 있다. 이를 활용하여 주어진 x, y가 해당 영역의 각 변을 직각 이등분 하는 직선을 기준으로 큰지 작은지 확인하면 4개의 작은 영역 중에 어디 속해있는지 알 수 있다. 2차원에서 진행하는 일종의 이분 탐색이라고 할 수도 있겠다.

x, y가 어느 영역에 속하는지 확인하는 코드는 다음과 같이 작성하였다. 뒤에 따라오는 그림과 함께 보자.

...
		num = 2 ** (N - 1)
		# 좌상단
    if x <= num and y <= num:
        position(N-1, x, y, base)
        
		# 우상단
    elif x > num and y <= num:
        position(N-1, x - num, y, 4 ** (N - 1) + base)
    
		# 좌하단
    elif x <= num and y > num:
        position(N-1, x, y - num, 2 * 4 ** (N - 1) + base)
        
		# 우하단
    elif x > num and y > num:
        position(N-1, x - num, y - num, 3 * 4 ** (N - 1) + base)

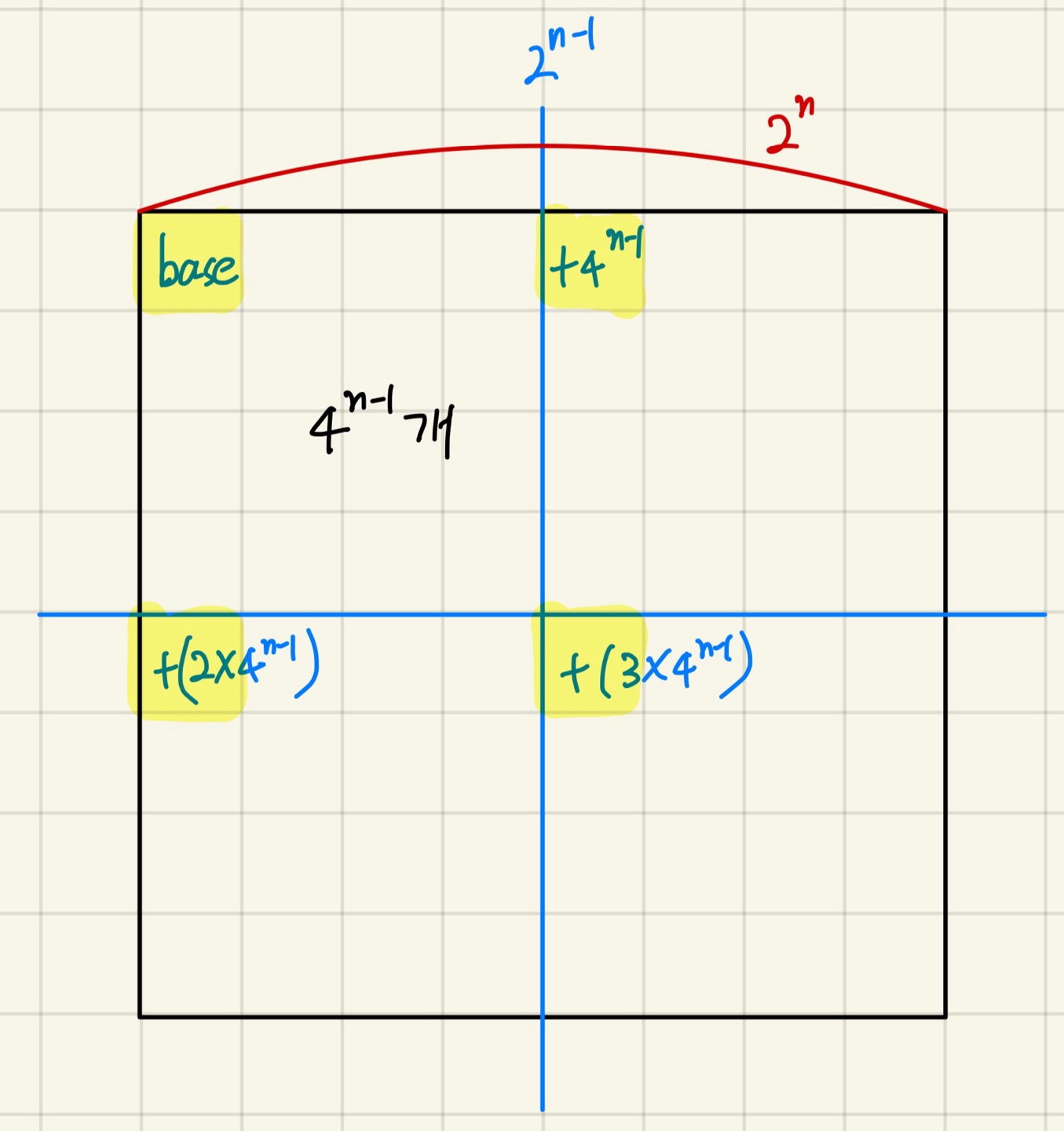
위와 같이 한 변이 $2^n$인 영역이 주어졌을 때 각 변을 직각 이등분 하는 선은 가장 좌상단의 꼭짓점에서 $2^n/2(=2^{n-1})$ 만큼 떨어져 있는 것을 확인할 수 있다. 그러므로 x, y가 $2^{n-1}$보다 큰지 작은지 확인하면 네 개의 영역 중 어디에 속해있는지 알 수 있다. 단 여기서 x는 커질수록 오른쪽, y는 커질수록 아래로 진행한다고 생각해야 한다.

base는 말 그대로 지금 확인하려 하는 영역의 기준 칸을 뜻하는 것으로 가장 좌상단에 위치하는 칸을 뜻한다. 그리고 이 base는 원하는 점이 어느 영역에 속하는 지에 따라 계속 바뀌어야 한다. 즉, 각 영역에 따라 노란색으로 칠한 칸이 다음 영역의 base가 된다. 그리고 이 base는 Z 순서에 따라 $base+0,base+(4^{n-1}),base+(2\times4^{n-1}),base+(3\times4^{n-1})$로 계산할 수 있다. 이는 작은 영역에 속한 칸의 개수가 $2^{n-1}\times2^{n-1}(=4^{n-1})$이기 때문이다.

코드

import sys
N, y, x = map(int, sys.stdin.readline().split())

def position(N, x, y, base=0):
    if N == 0 or (x <= 1 and y <= 1):
        print(base)
        return base
    
    num = 2 ** (N - 1)
    if x <= num and y <= num:
        position(N-1, x, y, base)
        
    elif x > num and y <= num:
        position(N-1, x - num, y, 4 ** (N - 1) + base)
    
    elif x <= num and y > num:
        position(N-1, x, y - num, 2 * 4 ** (N - 1) + base)
        
    elif x > num and y > num:
        position(N-1, x - num, y - num, 3 * 4 ** (N - 1) + base)
        
position(N, x + 1, y + 1)

위에서 설명한 알고리즘을 따라 계속 진행한다. 다만, 설명할 때는 x, y값이 변하지 않는 것으로 생각하고 진행했지만 편의를 위해 x, y 중 변하는 좌표에 $2^{n-1}$를 빼며 진행하였다. 필요 없는 영역을 잘라내면서 진행한다고 생각하면 된다. x, y의 값이 실제와 달라져도 base의 값만 알맞게 계산하면 정답을 찾아낼 수 있다.

N이 0이 되거나 x, y가 모두 1 이하이면 찾으려는 칸에 도달했다는 뜻이므로 답을 출력하고 중지한다.