Backpropagation

---

Backpropagation

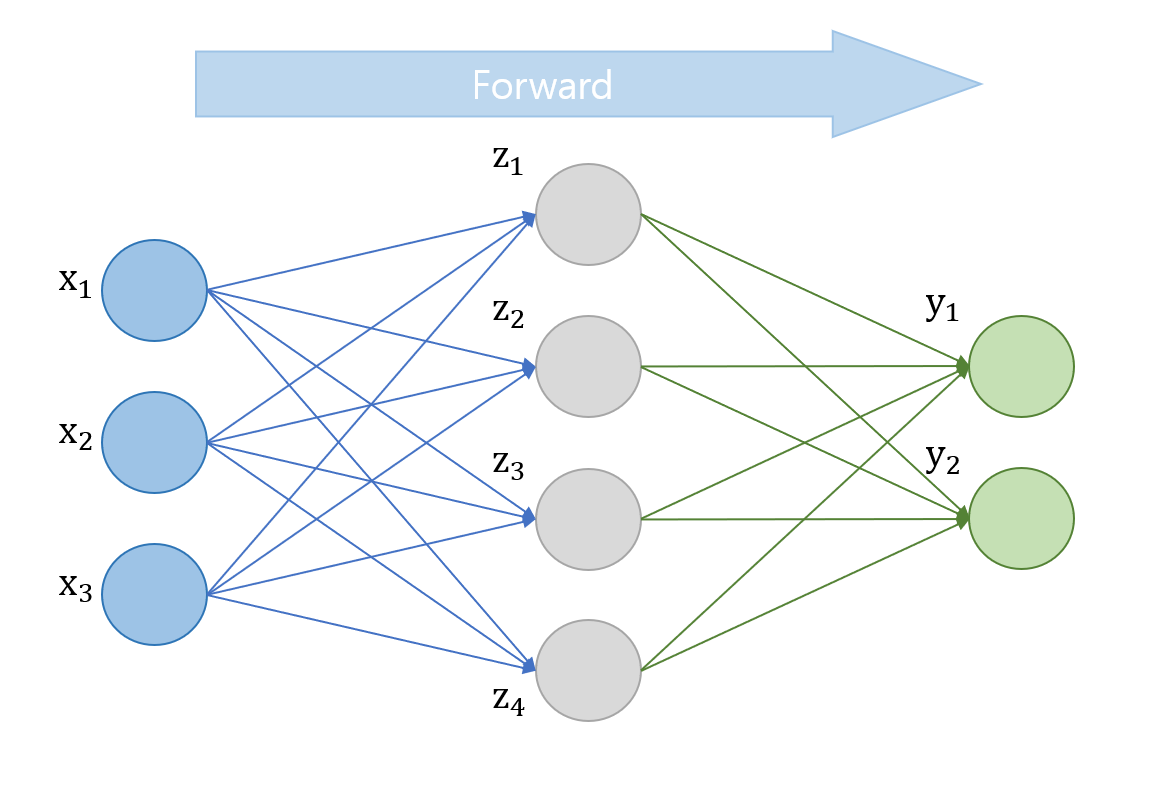
데이터를 레이어의 노드들을 통과시키면서 설정된 weight에 따라 예측 결과값을 계산하는 것을 forward pass라고 한다.

MLP의 결과값을 만들어 주는 필수적인 과정이지만 이것만으로는 weight를 개선하면서 학습을 진행할 수가 없다.

이것을 가능하게 해준 것이 바로 backpropagation(오차 역전파)이다.

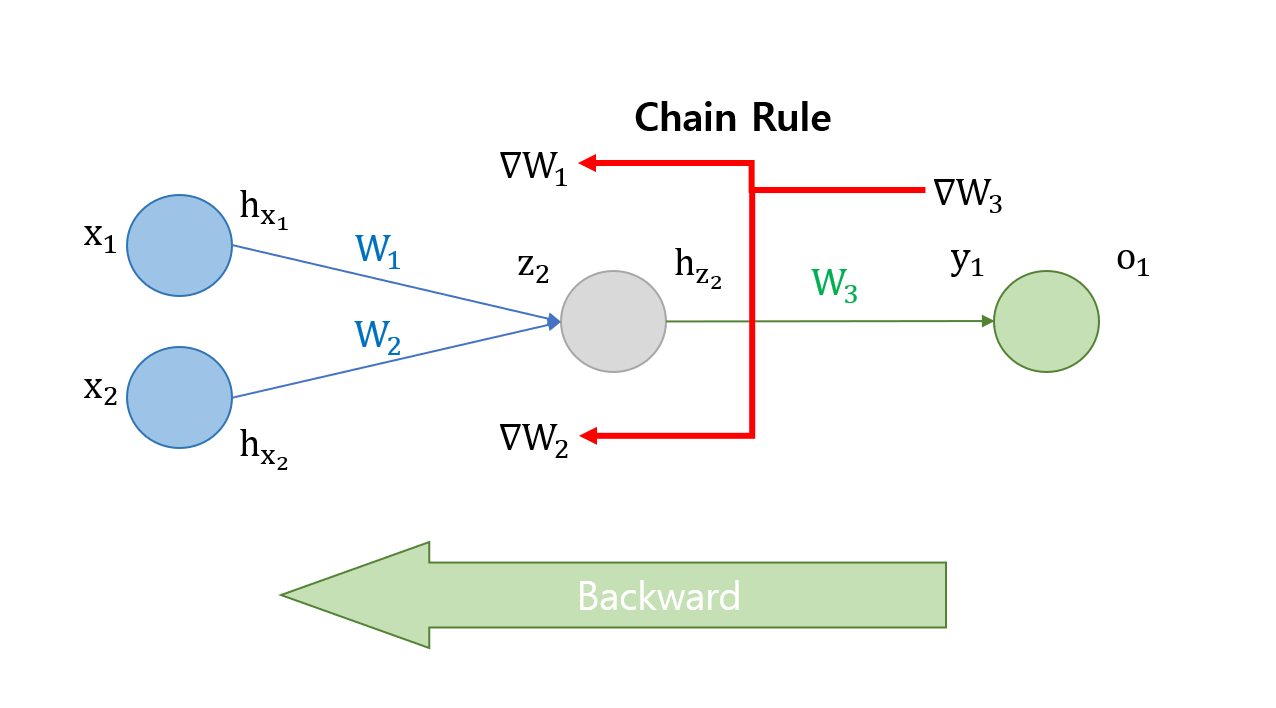
역전파 알고리즘은 chain rule을 통해 각 노드들에 prediction과 target의 total error를 전달하여 $\nabla W$를 계산할 수 있게 해 준다. 오차 역전파라는 이름이 붙은 것도 이 때문이다.

이렇게 계산한 $\nabla W$를 사용하여 다음과 같이 weight를 개선한다.

\[W:=W-\alpha\nabla W\]

자세한 내용은 관련 포스팅을 참고하자

위에서 나왔던 네트워크의 일부분을 떼서 역전파가 어떻게 적용되는지 확인해 보자.

먼저 최종 output에 가장 가까운 $\nabla W_3$부터 계산한다.

\[\nabla w_3=\frac{\partial cost}{\partial W_3}=\frac{\partial cost}{\partial o_1}\frac{\partial o_1}{\partial y_1}\frac{\partial y_1}{\partial W_3}\]

$\nabla W_3$는 chain rule을 통해 위와 같이 미분이 바로 되는 형식으로 표현할 수 있다. 한 번 더 거슬러 올라가 보자.

이번에는 $\nabla W_1$과 $\nabla W_2$를 구할 차례이다. 먼저 $\nabla X_1$을 구해보자.

\[\frac{\partial cost}{\partial W_1}=\frac{\partial cost}{\partial y_1}\frac{\partial y_1}{\partial h_{z_2}}\frac{\partial h_{z_2}}{\partial z_2}\frac{\partial z_2}{\partial W_1}\]

마찬가지로 chain rule을 통해 계산한다. $\frac{\partial cost}{\partial y_1}$은 $\nabla X_3$을 구할 때 구했었기 때문에 모든 편미분이 계산 가능하다.

$\nabla W_2$는 여기서 $W_1$을 $W_2로 바꿔주기만 하면 된다.$

\[\frac{\partial cost}{\partial W_2}=\frac{\partial cost}{\partial y_1}\frac{\partial y_1}{\partial h_{z_2}}\frac{\partial h_{z_2}}{\partial z_2}\frac{\partial z_2}{\partial W_2}\]

최종 output이 없어도 forward 도중에 계산할 수 있는 편미분들은 forward pass를 하면서 미리 계산하여 저장해 두고 사용한다.

이번 예제에서는 아주 간단한 네트워크에 대해 다뤘지만 더 깊고 넓은 네트워크에 대해서도 똑같이 적용할 수 있다.