오토인코더의 모든 것 - 3. Autoencoders
이활석님의 오토인코더의 모든 것 강의를 본 후 공부 및 정리를 목적으로 작성한 게시물임을 알려드립니다.
Introduction
Autoencoder
오토인코더는 인폿과 아웃풋이 같은 네트워크를 의미한다. Auto-associators, Diabolo nerworks, Sandglass-shaped net 등의 이명으로 불리기도 하며 가장 많이 불리는 이름은 역시 Autoencoder이다.
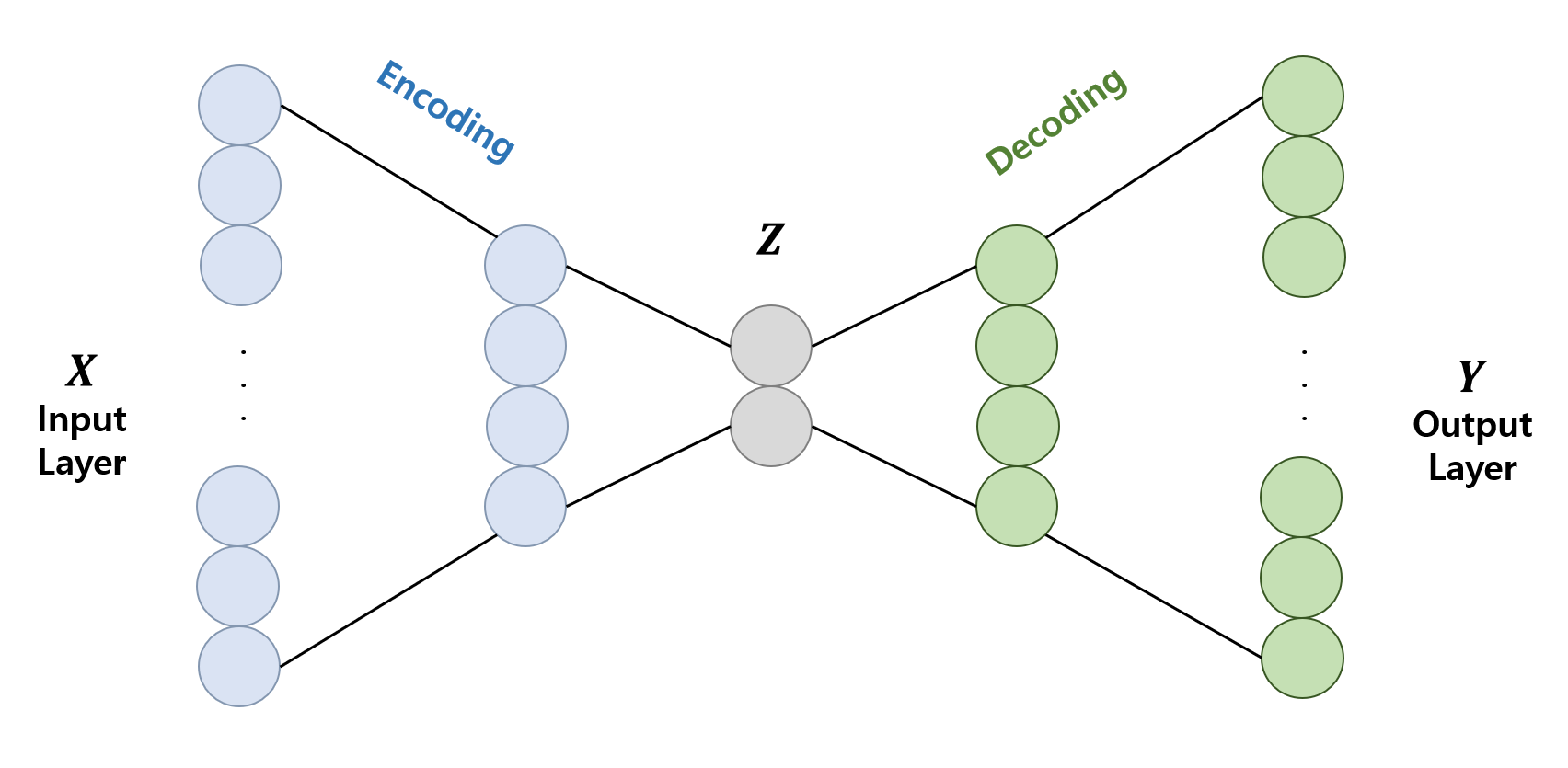
오토인코더는 다음과 같이 중간의 은닉층이 잘록한 모습의 네트워크인데, 이때 중간 은닉층을 $Z$라고 부르며 Code, Latent Variable, Feature, Hidden representation 등으로 불린다. 그래서 $Z$를 어떻게 생각하냐에 따라 오토인코더에서 학습하는 과정을 Representation Learning, Efficient Code Learning 등으로 부르기도 하지만, 결국 이들은 모두 $Z$ 노드를 배우는 학습을 이르는 말들이다.
처음 오토인코더가 각광받은 이유는 unsupervised learning 문제인 Demension Redection을 supervised learning으로 바꿔 풀 수 있다는 개념 때문이었다. 최종 출력물이 원래의 입력과 같은 문제로 보고 학습을 한 후에, encoder 부분만 떼서 사용하면 차원축소가 가능한 네트워크를 얻을 수 있기 때문이다.
이 경우 자기 자신에 대해 학습(self learning)하기 때문에 적어도 training DB에 있던 것들에 대해서는 압축을 잘 해준다. 즉, 최소 성능이 어느정도 보장된다는 장점이 있다. 하지만 같은 이유로 새로운 것을 생성하려 해도 기존의 DB와 비슷한 결과가 많이 나온다는 평가를 듣기도 하였다.
General AE(AutoEncoder) and Linear AE
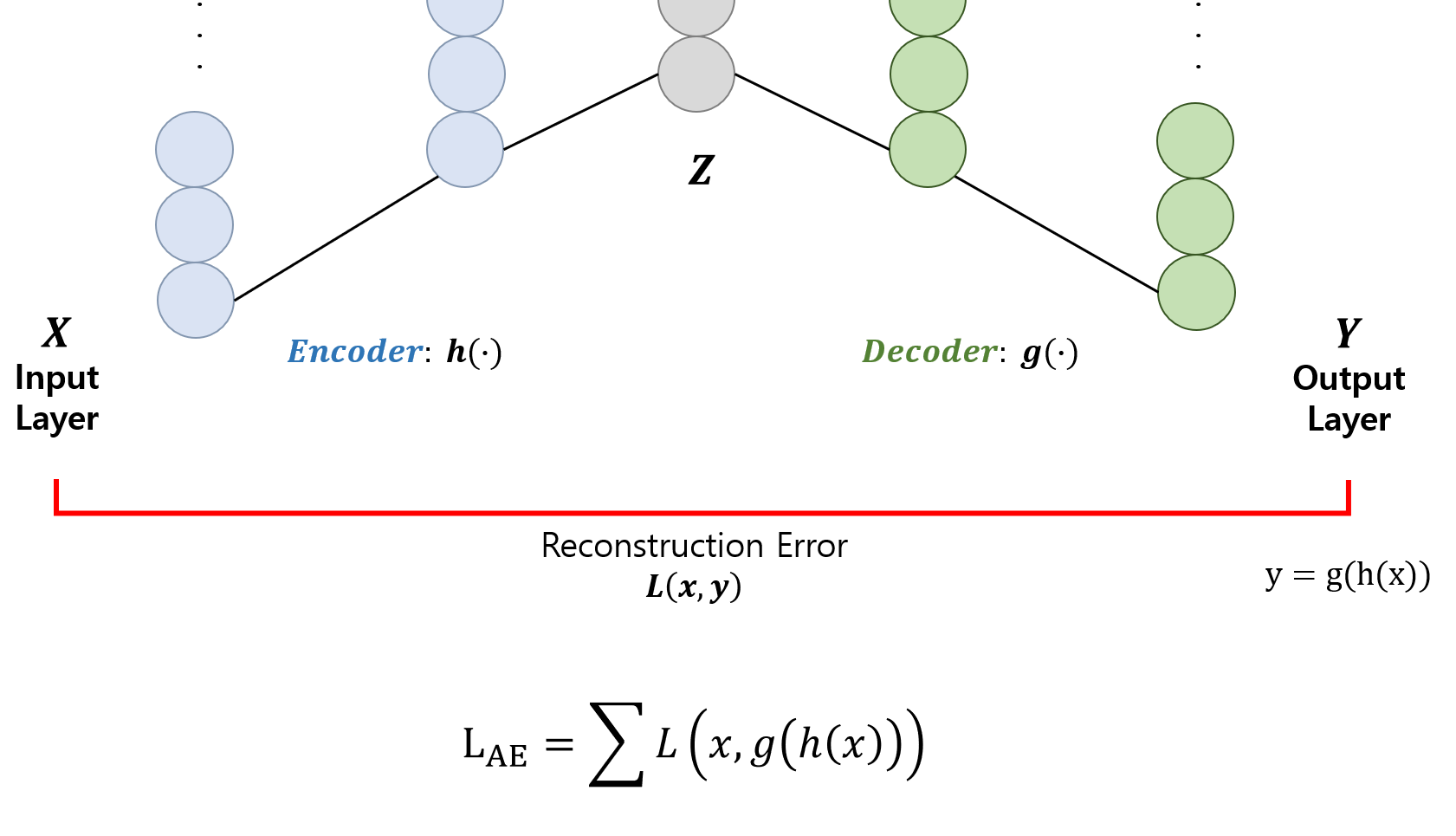
General AE를 조금 더 자세히 보자. 위에 나왔던 그림을 자세히 나타내면 다음과 같다.
최종 출력 $Y$는 인코더의 출력은 디코더에 인풋으로 넣어 나온 output으로 정의할 수 있고, 이것이 첫 input $X$와 같기를 바라므로 이들끼리의 error를 구한다. 이때는 데이터의 분포 형태에 따라 MSE 또는 cross-entropy를 사용한다. 이렇게 구한 error를 재구축(reconstruct) 한 것에 대한 error라는 의미로 Reconstruction Error라고 한다.
Linear AE는 기본적인 오토인코더의 구조에서 은닉층을 활성화 함수 없이 선형 함수를 그대로 사용한 것을 말한다. PCA(Principle Component Analysis)와 baisis는 다르지만 선형적으로 차원 축소를 진행하기 때문에 결과적으로 PCA와 같은 mainifold를 학습한다는 특징이 있다.
Pretraining
Stacking AE
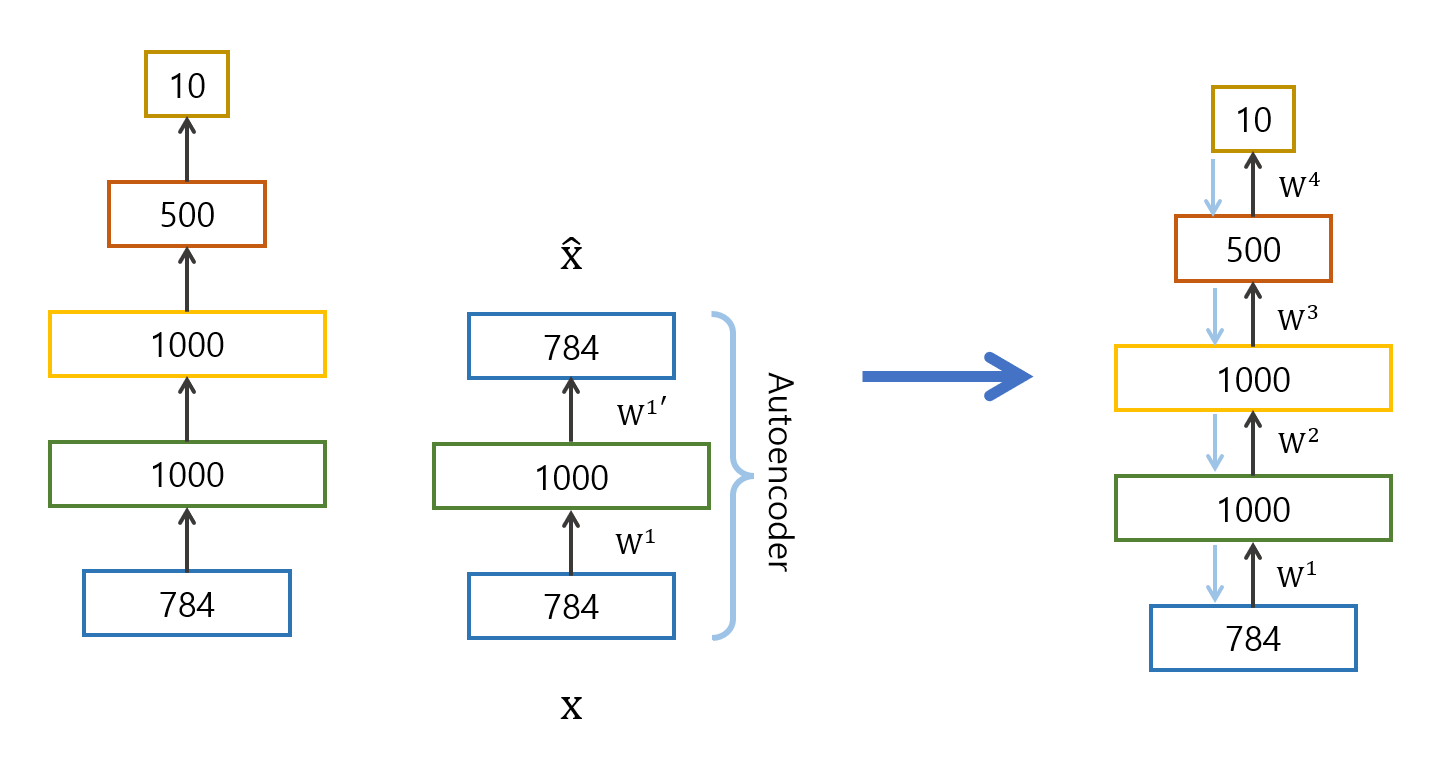
현재의 CNN, DNN 방법론들에 비해 예전의 방법론들은 적절한 parameter 초기화가 어려웠다. 이때 오토인코더로 pretraining을 하니 성능 개선이 이루어졌다고 해서 사용되기 시작한 방식이다. pretraining 방식은 다음과 같다.
먼저 원하는 차원으로 보낸 후, 원래 레이어로 돌아와서 제대로 복구가 되는지 확인한다. 이 과정에서 오토인코더 구조가 사용된다. 적어도 input layer의 값들을 복구할 수 있는 prameter를 사용하자는 것이다. 이 과정을 모든 레이어에 대해 진행하면서 prameter를 고정한다.
학습이 모두 끝난 뒤에는 random inintialization으로 backpropagation한다.
DAE(Denoising AE)
원래의 오토인코더 방식으로 학습을 하되 input 데이터에 noise를 추가하여 학습하는 방식이다. 이때 핵심은 noise를 (이미지 같은 것을) 사람이 봤을 때 다르지 않을 정도만 추가한다는 것이다.
이런 식으로 학습을 하면 사람이 봤을 때 같은 것(manifold상 거의 같은 것)이 무엇인지 학습할 수 있게 된다는 concept이다.

Stochastic Contractive AE(SCAE)
DAE에서 loss의 의미를 해석하여 다르게 표현한 것이다. DAE의 loss를 생각해 보면 $g$, $h$중 $h$는 특히 데이터가 조금만 바뀌1어도 manifold 상에서 같은 smaple로 매칭이 되게 학습을 해야 한다고 볼 수 있다. 이 의미를 재구성 해보면 다음과 같이 적을 수 있다.
reconstruction error를 통해 원래 오토인코더의 형태대로 입출력이 동일하게 학습하고, stochastic regularization항을 통해 manifold 상에서 거리가 같게 학습하도록 loss를 구성하였다.
CAE
SCAE의 stochastic regularization 항을 테일러 전개를 통해 근사하여, Frobenius norm 형태로 만들어, analytic regularization로 적용한 것이 CAE이다. 하지만 1차 미분 항에서 끊어 근사한 것이므로 한 지점의 근처에서만 유의미한 근사가 된다고 할 수 있다.
위 식으로 regularization 항을 대체하여 다음과 같이 CAE loss를 적용한다.
DAE vs CAE
결국 DAE와 CAE의 concept 자체는 mainfold 위의 거리를 줄인다는 것으로 같지만, 그것을 적용하는 방식이 달랐다.
DAE의 경우 noise가 첨가된 input으로 학습하여 manifold 상의 거리를 좁히려 했다면, CAE는 regularization을 통해 이를 해결하려 했다.
실제로는 CAE보다 DAE가 더 많이 쓰인다고 한다. 참고로 AE, DAE, VAE(Variational AE)가 많이 쓰이는 오토인코더 종류라고 한다.