KL divergence(쿨백-라이블러 발산)
Related Post
- Entropy
- KL Divergence
- Cross Entropy
이번에는 엔트로피에 이어 쿨백-라이블러 발산(Kullback-Leibler divergence)에 대해 알아보려 한다.
Kullback-Leibler divergence, KLD
쿨백-라이블러 발산은 어떤 두 확률분포의 차이를 계산하기 위한 함수로, 두 확률분포의 정보 엔트로피의 차이를 계산한다.
의미적으로는 확률분포 $P$가 있을 때 그 분포를 근사적으로 표현하는 $Q$를 $P$ 대신 이용하여 샘플링 할 경우 엔트로피의 변화를 의미한다.
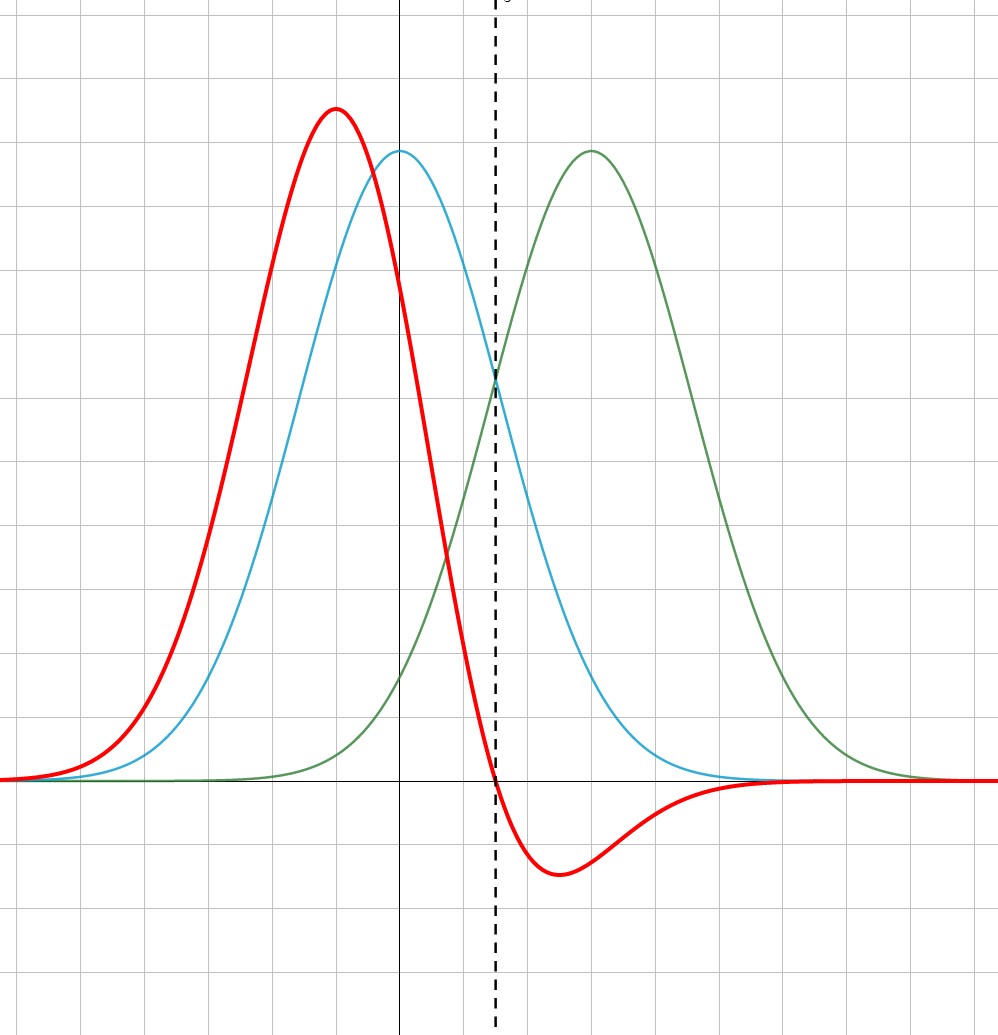
시각적으로도 한번 확인해 보자. 여기 확률분포 $P$(파란색)와 $Q$(초록색)가 있다. 그리고 두 확률분포에 대한 엔트로피 차이를 계산하여 표현한 곡선(빨간색)을 볼 수 있다.
그래프에서 확인할 수 있듯이 (당연하게도) 분포간의 차이가 큰 곳에서는 엔트로피의 차이가 크고 차이가 적은 곳에서는 줄어든다. 심지어 두 확률분포의 교점(점선)에서는 값이 같기 때문에 엔트로피의 차이도 0이 되는 것을 확인할 수 있다.
이제 수식으로도 한번 표현해 보자. $P$의 엔트로피는 다음과 같고
\[ H\left( P \right)= -\sum^n_{i=1} p\left( x_i \right) \log{ p\left( x_i\right ) } \]
$P$대신 $Q$를 사용하여 샘플링할 경우 엔트로피는 다음과 같이 정의된다. ($Q$의 정보량에 대한 기댓값)
\[ H\left( P, Q \right)= -\sum^n_{i=1} p\left( x_i \right) \log{ q\left( x_i\right ) } \]
쿨백-라이블러는 이들의 차이라고 했으므로 다음과 같이 정의할 수 있다.
$ KL\left( P||Q \right) = H\left( P, Q \right) - H\left( P \right) $ $ = \left( -\sum^n_{i=1} p\left( x_i \right) \log{ q\left( x_i\right ) } \right) - \left( -\sum^n_{i=1} p\left( x_i \right) \log{ p\left( x_i\right ) } \right) $ \[ = -\sum^n_{i=1} p\left( x_i \right) \log{ \frac{ q\left( x_i\right )}{ p\left( x_i\right ) } } \]
이때 이산확률분포의 쿨백-라이블러 발산은 위에서 표현한 것과 같이 총 합으로 나타낼 수 있으며 다음과 같고
\[ KL\left( P||Q \right) = \sum_i P\left( i \right) \log{ \frac{ P\left( i \right )}{ Q\left( i \right ) } } \]
연속확률분포의 쿨백-라이블러 발산은 적분 값으로 주어진다. (이때 $p, q$는 각 확률분포의 확률밀도 함수이다.)
\[ KL\left( P||Q \right) = \int^\infty_{-\infty} p\left( x \right) \log{ \frac{ p\left( x \right )}{ q\left( x \right ) } }dx \]
엔트로피와 쿨백라이블러 발산을 알아봤으니 이어서 다음 포스팅은 cross entropy 내용에 대해 알아보도록 하겠다.